Загальна характеристика наукового дослідження 4 страница

Порядкове вимірювання можливе тоді, коли дослідник може виявити в предметів відмінність ступенів якості або ознаки. У цьому випадку числа приписуються предметам таким чином: якщо число, присвоєне предмету А, більше числа, присвоєного предмету В, то це значить, що в А дана якість виражена більше, ніж у В. Порядкове вимірювання назива­ють ранжуванням, тобто приписуванням рангів (або місць).

Наприклад:

Маємо 10 студентських груп. Після вимірювання рівня розвитку міжособистісних відношень у кожній із цих груп в залежності від зайнятого місця розташовуємо групи в порядку від 1 до 10. Це є одна властивість, але з різним ступенем її вираження. Іншим прикладом може виступати роз поділ цінностей за рангами залежно від їх значущості для досліджуваного.

Загальні характеристики та приклади вимірювальних шкал надане в табл. 2.3.

Шкали порядку часто виступають основними, а іноді й єдиними, для оцінювання об'єктів. Більша частина шкал, які використовуються в психолого-педагогічному дослідженні — це шкали порядку. Порівняно шкалами найменувань шкали порядку мають важливі нові властивості вони встановлюють відношення "більше-менше" між об'єктами за будь якою властивістю, тобто встановлюють порядок, послідовність. Збільшуються і можливості статистики: при використанні рангових шкал може бути здійснений розрахунок медіани, відсотків, ранґової кореляції.

Шкала інтервалів передбачає присвоєння чисел об'єктам, коли од­накові різниці чисел відповідають однаковим різницям значень вимірюваної ознаки або властивості об'єкта. Основна особливість інтервальних шкал — це довільність вибору відмітки "0" на шкалі, яка зовсім не озна­чає повної відсутності вимірюваної якості. Головна проблема при побу­дові шкал інтервалів в психолого-педагогічному дослідженні полягає н обґрунтуванні рівності між пунктами шкали.

Шкала відношень виступає шкалою вищого порядку; вона показує, що відношення між двома об'єктами дорівнює відношенню між двома іншими, як і дорівнюють числа, що приписуються об'єктам з такими ж властивостями. Шкала відношень, у порівнянні зі шкалою інтервалів, доповнюється об'єктивністю нуля. Нуль у цій шкалі означає повну відсутність властивості, що вивчається. Дослідник у цьому випадку завжди може сказати, у скільки р у досліджуваного А вимірювана властивість більше, ніж у вивчаючого В.

За допомогою шкали відношень здійснюються вимірювання в психофізіологічних дослідженнях, де одиницями вимірювання є фізичні величин прикладом перемінних, які вимірюються в шкапах відношень, можуть бути: з вага, висота звуку, час на вирішення завдань або вивчення списку слів.

Шкалам відношень притаманні й власні прийоми статистики: сере геометричне, коефіцієнт варіабельності, логарифмічне перетворення.

Психологічні тести часто містять у собі кілька типів шкал.

Наприклад:

Окреме питання тесту Айзенка має номінальну шкалу (можна від вісти "так" або "ні"), складання відповідей здійснюється згідно з при щенням шкали інтервалів.

Можливими є перетворення з однієї шкали в іншу. Результати, отримують за шкалою інтервалів, можуть бути перетворені в ранґи переведені в номінальну шкалу.

Вдалий приклад такої інтерпретації даних з використанням первинних результатів 6 досліджуваних за шкалою екстраверсії — інтроверсії тесту Айзенка, наведених С.Г. Тарасовим, надано в табл. 2.4

Таблиця2.4.

Перший стовпчик – імена тих, хто досліджувався; другий стовпчик – бал за вираженість якості (реалізована шкала інтервалів); третій стовпчик – згідно з початковим балом тим, хто досліджувався, приписаний ранг – той, хто має наступний за величиною бал і т.п.); четвертий стовпчик – згідно з початковими балами ті, хто досліджувався, розподілені на два класи: інтроверти (І) – бали від 0 до 12, екстраверти (Е) – від 13 до 24.

Кожного разу при переході від однієї шкали до іншої губиться частина інформації про тих, хто бере участь в експерименті. Так, при ранжуванні розміщуються один за одним учасники Д і Е, в яких різниця початкових балів дорівнює 1, а також учасники Г і Б, різниця початкових балів яких складає 6. При розподілі учасників за класами до одного класу належать учасники, в яких первинні оцінки дуже відрізняються.

Слід пам'ятати, що кожен спосіб обробки експериментальних даних розрахований на певний тип шкал. Використання математичних методів до неадекватних даних призводить до одержання дивних або навіть помилкових результатів. Тому досліднику важливо чітко уявляти, з яким типом шкали він працює, бо вся подальша математична обробка результатів визначається типом вимірювальної шкали.

У психолого-педагогічних дослідженнях часто використовуються різні числа.

Принципи та методи обробки результатів досліджень

Числа (змінні), що є результатом вимірювань, називаються варіантами (вони варіюються, тобто змінюються) і позначаються Х_і. Всі значення змінної, які розташовані в один ряд у порядку зростання або зменшення, утворюють варіаційний ряд. Кількість повторень однакових результатів у складі варіаційного ряду називається частотою даного значення змінної (n).

Уявимо, що викладач має відповіді 36 студентів курсу на питання анкети «Як часто твої погляди і смаки співпадають з поглядами і смаками твоїх однокурсників?". Передбачалося 5 категорій відповідей: завжди, часто, інколи, досить рідко, ніколи. Для обробки матеріалів перш за все необхідно приписати категоріям відповідей цифри 5,4,3, 2, 1, а далі скласти варіаційний ряд і таблицю частоти відповідей. Ця процедура дає можливість визначити ступінь згоди студентів відносно запропонованого для оцінки судження. Розмістивши ряд відповідей у порядку зменшення значень змінної, отримаємо такий варіаційний ряд: 5,5,5,5,5,5,5,5,5,4,4,4,4,4,4,3,3,3,3,3,3,3,3,3,3,3,3, 3, 2, 2, 1, 1, 1, 1, 1, 1, 1. Для зручності математичної обробки всі відповіді студентів вміщують у таблицю (табл. 2.5).

Частота відповідей студентів Таблиця 2.5

	Варіанти	Всього варіантів
Частоти	Завжди (5)	Часто (4)	Інколи (3)	Досить рідко (2)	Ніколи (і)

Такий ряд легко уявити і графічно.

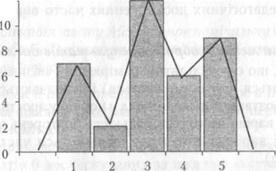Згідно вибраному масштабу на горизонтальній осі відкладаються варіанти, на вертикальній — їх частоти. Такий графік називається гістограмою частот. Висота кожного стовпчика в ньому строго пропорційна дійсні частоті кожного значення заміру (варіанти) і дорівнює частоті даного значення, а площа всього багатокутника дорівнює числу зроблених замірів (варіант). З метою більшої наочності гістограму можна видозмінити в полігон частот (тобто замість контуру багатокутника одержати криву розподілу). Для цього потрібно опустити середні ординати в кожному стовпчику частот кожного значення і об'єднати лінією їх вершини (див. рис).

Частота 12

Варіанти

Рис. Гістограма і полігон частот варіаційного ряду відповідей студентів на питання анкети

На одній осі координат можна зобразити декілька кривих розподілу, якщо вони одного і того ж значення (криві при цьому краще зробити кольоровими). Це дає можливість наочно побачити, в чому схожість або відмінність у прояві одних і тих же ознак, наприклад, у різних первісних груп.

Характеристиками варіаційного ряду виступають середня арифметична і медіана. Вони показують наскільки єдиними, подібними, однорідними є отримані дані (в нашому прикладі — відповіді студентів на питання анкети).

Середня арифметична (середнє значення або вибіркове середнє дорівнює сумі всіх значень варіанти, поділеної на кількість членів варіаційного ряду (п). Вона визначається за формулою:

Якщо серед членів деякі варіанти повторюються (як в нашому при кладі), то середню цього ряду називають середньоарифметичною зваже пою і визначають за формулою:

де Х_n — варіанта, ознака;

К_n — вага (частота) варіанти.

Використовуючи дані таблиці частот відповідей студентів, визначи­мо величину середньоарифметичної зваженої

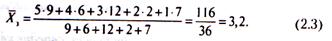Величина середньоарифметичної зваженої X₃ = 3,2 свідчить про те, що для досліджуваної групи в цілому не є характерним збіг поглядів і смаків кожного окремого студента. Вони співпадають лише інколи, хоча невели­кії тенденція змін відповідей в напряму оцінки спостерігається.

На величину 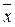значно впливають крайні величини ряду. Тому для усунення такого впливу застосовується й інший спосіб визначення се­редньої величини — знаходження медіани (Med).

Медіана — це така величина варіаційного ряду, яка займає його се­редину. Щоб визначити медіану, потрібно знайти, від якої варіанти буде однакова кількість як великих, так і менших вимірів. Місце розташуван­ня нього значення варіанти визначається за формулою:

(2.4)

де п — число членів ряду.

Якщо у варіаційному ряду число варіант є парним, то місце медіани розташоване між сусідніми вимірами і їх середнє значення потрібно взя­ти за величину медіани. У даному прикладі в ряду 36 варіант. Місце ме­діани, згідно з формулою, дорівнює 18,5 варіанти (виміру) від початку ряду. Отже, необхідно скласти сусідні 18 і 19 варіанти і середню їх вели­чину взяти за величину медіани

(2.5)

У порівнянні із середньоарифметичною зваженою, зміна любої час­тини ряду не так різко позначається на медіані, і тому медіана вважаєть­ся найбільш представницькою мірою ряду. У нашому прикладі різниця між середньоарифметичною зваженою і медіаною складає 2/10, що в пев­них випадках може мати суттєве значення.

Середня арифметична і медіана, виступаючи основними характерис­тиками варіаційного ряду (інколи використовується і мода, яка відпові­дає найбільшій частоті ряду), усе-таки не можуть відобразити всі йог особливості.

У психолого-педагогічних дослідженнях завжди виникає необхідиість у більш глибокому аналізі одержаних даних. Тому математична статистика пропонує й інші характеристики варіаційного ряду, які показують як групуються окремі варіанти навколо середньої, яка їх тіснота і ступінь відхилення від неї. Ці показники надають можливість також порівняти між собою результати, що отримані на різних об'єктах дослідженн (різних вибірках).

Такими характеристиками є дисперсія, середнє квадратичне відхилення і коефіцієнт варіації.

Без уміння оперувати цими величинами неможливе визначення рівня надійності й достовірності будь-якого проведеного дослідження.

Дисперсія (σ²)— це міра розсіювання варіант (ознак) навколо середньої. Вона вказує, наскільки тісно зв'язані між собою ознаки і наскільки кожна з них відрізняється від середньої величини. Дисперсія визначається за схемою:

1. Від кожної варіанти х_і віднімається середня арифметична х:

(2.6)

2. Різниця підноситься до квадрату і множиться на частоти (n_і):

(2.7)

3. Отримані дані складаються:

(2.8)

4. Сума поділяється на число варіантів ряду (n). Одержане число і називається дисперсією (сигма в квадраті)

(2.9)

Однак операції з дисперсією будуть значно спрощені, якщо із неї до­бути квадратний корінь. Ця величина називається середнім квадратич­ним відхиленням σ:

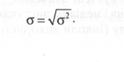(2.10)

Для знаходження дисперсії і середнього квадратичного відхилення кди складаються таблиці.

Таблиця 2.6

Дані для розрахунку дисперсії

хі	(хі-х)	(хі-х)^2	(хі-х)^2∙ пі
	5-3,2- 1,8	3,24	29,16
	4 - 3,2 = 0,8	0,64	3,84
	3 - 3,2 = - 0,2	0,04	0,48
	2-3,2-- 1,2	1.44	2,88
	1 - 3,2 - - 2,2	4,84	33,88 ∑ = 70,24

Визначаємо дисперсію:

(2.11)

Це дозволяє зробити розрахунок середнього квадратичного відхи­лення:

Кофіцієнт варіації (n) показує, яку частину становить середнє квадратичне відхилення від середньої арифметичної. Він обчислюється за формулою:

Коефіцієнт варіації дозволяє порівнювати між собою різні варіаційні ряди і більш глибоко розібратися в закономірностях кожного ряду. У математичній статистиці прийнято вважати, що ті показники, ко­ефіцієнт варіації яких достатньо малий (10-15 %), представляють собою стабільні характеристики. Якщо він більше 40 % (як у нашому прикладі), то це означає, що варіаційний ряд суперечний, його варіанти (ознаки) неоднорідні.

Методи вивчення взаємозв'язків психолого-педагогічних явищ

Міри зв'язку між змінними

Зв'язки (залежності) між двома або більше змінними в статистиці на­зивають кореляцією. Вона оцінюється за допомогою коефіцієнта кореляції. Коефіцієнт кореляції є мірою ступеня та величини цього зв'язку.

Наприклад:

Необхідно виявити залежність успішності навчання від відвідування студентами лекцій.

Існує багато коефіцієнтів кореляції. Вони визначаються типом зв'язку між змінними.

Міри зв'язку для явищ, які вимірюються в номінальних шкалах

Найпростішим випадком номінальної шкали є дихотомічна, тобто шкала, яка виділяє два класи в одному явищі. Визначення коефіцієн та кореляції зручно здійснювати за допомогою таблиці сполучення (табл. 2.7), яка показує кількість сумісного виникнення пар значень за двома ознаками.

Загальна форма таблиці сполучення Таблиця 2.7

Ознака Y	Ознака X	Всього
	А	В	А + В
	С	А	С+Д
Разом	А+С	В+Д	N

Можливими варіантами сполучень двох змінних є:

А — кількість випадків, коли змінна X має значення 0, і одночасно змінна У має значення, яке дорівнює 1;

В — кількість випадків, коли змінні X і У мають одночасно значення, які дорівнюють 1;

С — кількість випадків, коли змінні X і У мають одночасно значення, що дорівнюють 0;

Д — кількість випадків, коли змінна X має значення, що дорівнює 1, і одночасно змінна У має значення, що дорівнює 0.

Такий зв'язок прийнято вимірювати за допомогою коефіцієнта коре­ляції Пірсона:

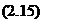
Наприклад:

Студент може відвідувати 50 % лекцій, а може і не відвідувати, студент може скласти залік з першого разу, а. може і не скласти.

Тоді таблиця буде мати такий вигляд:

Використовуючи формулу та дані таблиці сполучення, визначаємо коефіцієнт кореляції Пірсона:

Якщо γ наближається до 0 — зв'язок відсутній, якщо значення (на­ближається до -1 або +1, зв'язок існує, при цьому не завжди можна дати змістовну інтеграцію позитивному або негативному зв'язку.

Міри зв'язку для явищ, що вимірюються в рангових шкалах

Коефіцієнт рангової кореляції в психолого-педагогічних досліджен­нях використовується тоді, коли ознаки, між якими встановлюється за­лежність, розрізняються за якістю, але показники цієї різниці не можуть оцінюватися за допомогою інтервальної шкали.

Вихідними даними для обчислення коефіцієнтів рангової кореляції вис­тупають списки впорядкованих змінних. Це є раціональним у випадках, коли:

• двоє учасників дослідження або один і той же учасник, але в різних умовах, ранжували показники і встановили наявність або від­сутність зв'язку між списками;

• при наявності впорядкованих за двома методиками даних встанов­люється схожість — відмінність методик (наприклад, при визначенні валідності методики).

Для вказаних цілей використовується коефіцієнт рангової кореляції Спірмена (R_s). Він обчислюється за формулою:

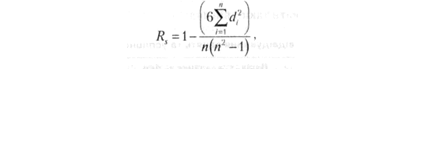де R_s — коефіцієнт рангової кореляції Спірмена;

d_і — різниця рангів об'єктів, що дорівнюються;

п — кількість об'єктів, що порівнюються.

Для прикладу розрахунку коефіцієнта Спірмена скористаємося да ними, наданими в табл. 2.9

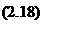
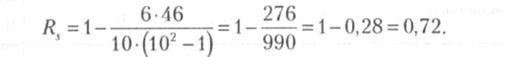
Значення коефіцієнта Спірмена змінюються від -1 до +1. У першо­му випадку між змінними, що аналізуються, має місце однозначний, але протилежно спрямований зв'язок: із збільшенням значень однієї змінної зменшуються значення іншої. У другому випадку — з ростом значень однієї змінної пропорційно зростає значення другої. Якщо величина R_s дорівнює 0 або має значення близьке до 0, то вагомий зв'язок між змінни­ми відсутній. Таблиця 2.9

Дані і проміжні результати обчислення значень коефіцієнта ранґової кореляції

Учасники дослідження	Ранги за методиками	Різниця рангів, d.	Квадрат різниці рангів, ?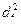
	№ 1	№2
В.М.
Г.В			-1
Н.П.			-3
Д.Л.
І.В.			-3
О.М.
М.В.
І.О.
P.C.
Т.В.
	=46

Міри зв'язку для явищ, що вимірюються в інтервальних шкалах

Найбільш поширеною мірою зв'язку виступає коефіцієнт кореляції (R_xy), який називають коефіцієнтом лінійної кореляції або добуток моментів Пірсона:

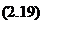
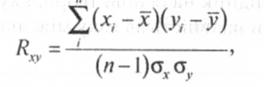де х_і,у_і— значення випадкових величин, які виміряні на і- тому об'єкті;

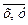— середні арифметичні величини х і у;

σ_х, σ_у — стандартні відхилення відповідних середніх величин;

п — кількість учасників, які досліджуються.

Досліджувані	х	у			()∙()
І.			- 1,5	+2,7	- 4,05
М.			+ 1,5	- 0,3	- 0,45
….	…	….	…	…	…
п			-0,5	- 1,3	+0,65

Послідовність розрахунків може бути представлена у вигляді таблиці 2.10.

Аналіз даних для розрахунку коефіцієнта лінійної кореляції Таблиця 2.10

Складання в останньому стовпчику таблиці виконується з урахуван­ням знака, тому R_xy може приймати як від'ємне, так і позитивне значення: -1 < R_xy< + 1. При використанні коефіцієнта кореляції як міри зв'язку необхідно враховувати, що він використовується у випадках нормального, двомірного розподілу, коли кожна випадкова величина, взята незалежно під іншої, має нормальний розподіл.

Позитивний знак коефіцієнта лінійної кореляції означає, що із збільшенням однієї змінної збільшується й інша, від'ємний, — що із збільшенням однієї — друга зменшується. У першому випадку в остан­ньому стовпчику таблиці будуть переважати позитивні числа, в другом випадку — від'ємні.

При використанні будь-яких мір зв'язку дослідник встановлює тіль один факт — є зв'язок чи його нема між двома змінними, чи змінюєть одна змінна разом з іншою або ні. Необхідно розуміти, що наявність зв'я ку ще нічого не говорить про її причину, про те, чим цей зв'язок мо бути обумовлений. Причина взаємозв'язку змінних може пов'язувати з однією із цих змінних, а може лежати далеко за межами явищ, що досліджуються. І тільки дослідник на основі теорії, яку він розроблює, мо пояснити і обґрунтувати наявність зв'язку між явищами.

Розділ III

СТРУКТУРА

І ЛОГІКА ПСИХОЛОГО-ПЕДАГОГІЧНОГО ДОСЛІДЖЕННЯ

3.1 Логічна структура дослідження

Ефективність наукового пошуку значною мірою залежить від пра­вильної послідовності дослідницьких кроків, що мають привести до істинних результатів, тобто від логіки дослідження.

Розробка логіки дослідження — процес дуже складний. Він не тільки передує, але і супроводжує весь процес дослідження, бо характер і послідовність кроків залежать від напряму і масштабів наукового пошуку, його цілей та завдань і багато в чому обумовлюються отриманими в процесі роботи результатами і труднощами, що виникають. Тому основну роботу і конструювання логіки психолого-педагогічного дослідження необхідно здійснити на початку цієї діяльності, спираючись па принцип моделювання кінцевого результату та ймовірних уявлень про ті етапи пошуків, які забез­печать його досягнення. Неможливо повною мірою уніфікувати і стандартизувати ці етапи, але основні кроки дослідника можна включити в структуру програми наукового дослідження, наведену в схемі 3.1.

1.Загальне ознайомлення з проблемою дослідження, обґрунтування її актуальності, рівня розробленості; визначення об'єкта і предмета, теми дослідження. Формулювання загальної і проміжних цілей дослідження.

2. Вибір методології — вихідної концепції, опорних теоретичних положень, єдиного задуму, дослідницького підходу, що визна­чає хід і передбачувані результати дослідження.

3. Побудова гіпотези дослідження — теоретичної конструкції, істинність якої мас бути доведено. Формулювання завдань, співвіднесених із цілями дослідження.

4.Вибір методів дослідження. Проведення констатуючого експерименту з метою установлення вихідного стану предмета дослідження. Складання робочого плану.

5.Збирання та нагромадження матеріалів дослідження. Органі­зація і проведення експерименту.

6.Аналіз, інтерпретація й оформлення результатів дослідження.

Схема 3.1. Структура програми психолого-педагогічного дослідження

Ці етапи (кроки) не тільки пов'язані між собою, але і взаємопроникають один в інший. Тому в ході наукової розробки дослідник повинен вно­сити ті чи інші, нерідко досить суттєві, корективи у виконану ним роботу по етапу, який уже здавався завершеним. Так, іноді доводиться уточнюва­ти цілі, задачі і план дослідження після того, як було отримане достатньо чітке уявлення про якісну характеристику одержаних у процесі роботи матеріалів. У процесі аналізу і узагальнення матеріалів дослідження може виявитися необхідність отримання додаткових даних. У цьому разі вико­навцю роботи необхідно знову повертатися до попереднього етапу.

До того ж, іноді важко провести чітке розмежування одного етапу дослідження від іншого.

Тому при конструюванні логіки наукового дослідження виділяють­ся основні частини: методологічна і процедурна.

Методологічна частина — від вибору теми до визначення задач і роз­робки гіпотези — значного мірою може здійснюватися за загальною для усіх дослідників логічною схемою:

проблема → тема → об'єкт → предмет → мета → наукові факти → → провідна ідея → гіпотеза → завдання дослідження

Логіка цієї частини наукового пошуку не є чітко однозначною, але значною мірою є заданою. Логіка другої частини роботи, процедурної, є заданою тільки в самому загальному вигляді:

упорядкування плану дослідження → опис методів і техніки збору даних, способу їхнього аналізу → проведення експерименту і перевірка гіпотез → аналіз, інтерпретація (пояснення), узагальнення одержаних результатів → конструювання попередніх висновків їх випробування і уточнення → формулювання заключних висновків

У кожному дослідженні необхідно знайти один із оптимальних варі­антів послідовності пошукових кроків, виходячи із характеру проблеми, предмета і задач дослідження, рівня оснащення роботи, можливостей дослідника та інших факторів. Але успіх будь-якого наукового дослі­дження залежить не тільки від того, як воно буде побудовано і методич­но забезпечено. Вирішальна роль тут належить самому досліднику і його відношенню до обраної ним теми наукової роботи.

3.2 Вибір і обґрунтування теми дослідження

Загальне ознайомлення з проблемою дослідження

Будь-яке психолого-педагогічне дослідження починається з теоре­тичного аналізу досліджуваної галузі педагогічної або психологічної науки, визначення проблеми, обґрунтування актуальності її розробки. Першим кроком дослідника є вибір об'єктивної галузі дослідження. Такою об'єктивною галуззю може бути або сфера практичної діяльності (наприклад, навчання певній дисципліні у фармацевтичному (медич­ному) навчальному закладі), або її відтворення у сфері наукової про­блематики (принцип неперервності в навчанні, суб'єктивно-діяльнісний підхід). Вибір об'єктної галузі визначається такими об'єктивними факторами, як її актуальність, новизна і перспективність, і суб'єктив­ними факторами: освітою, життєвим досвідом, інтересами, здібностя­ми, схильностями дослідника, його зв'язком з певним науковим колек­тивом і керівником.

Дата добавления: 2014-11-08