Доведення. Нехай дана зліченна множина , – її нескінченна підмножина

Доведення.

Доведення.

Нехай дана зліченна множина 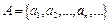, 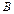– її нескінченна підмножина.

Нехай – перший елемент з послідовності 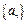, який належить 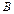; поставимо йому у відповідність число 1. Нехай – наступний елемент з послідовності 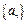, який належить 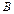; поставимо йому у відповідність число 2 і т. д.

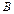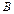Одержимо взаємно однозначну відповідність між і множиною натуральних чисел . Значить, множина за означенням є зліченною.

Теорема 2. Будь-яка нескінченна множина містить зліченну підмножину.

Нехай 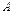- нескінчена множина. Візьмемо довільний елемент із множини 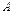і назвемо його . Далі візьмемо , і т. д. Одержимо послідовність , причому . Одержана підмножина множини 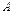є зліченною за побудовою.

Теорема 3. Об’єднання зліченної множини зліченних множин є зліченною множиною.

Нехай 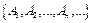– послідовність зліченних множин, і .

Розглянемо таблицю

Перенумеруємо елементи множин в такому порядку

Якщо в різних множинах 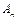, 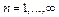зустрінуться однакові елементи, будемо рахувати їх тільки один раз. Таким чином, всі елементи множини 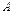перенумеровані і, отже, множина 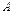є зліченною.

Теорема 4. Множина раціональних чисел є зліченною.

Доведення проводиться аналогічно доведенню теореми 3.

Теорема 5. Існують незліченні множини.

Дата добавления: 2014-11-20