
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доведення. Довести методом математичної індукції наступну рівність:
|
|
|
|
Приклад.
Довести методом математичної індукції наступну рівність:
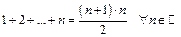 .
.
Перевіримо, що ця рівність правильна при 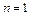 .
.
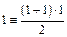 .
.
Припустимо, що рівність правильна при  , тобто
, тобто
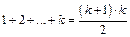 .
.
Доведемо, виходячи з цього, що рівність правильна при 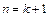 , тобто
, тобто
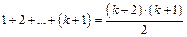 .
.
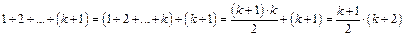 .
.
Значить, твердження має місце при будь-якому натуральному 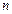 .
.
1.6. Біноміальні коефіцієнти. Біном Ньютона
Розглянемо два натуральних числа 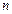 і
і 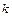
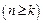 . Біноміальні коефіцієнти визначаються рівністю:
. Біноміальні коефіцієнти визначаються рівністю:
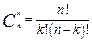 .
.
Мають місце наступні рівності:
1. 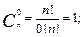
2. 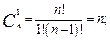
3. 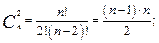
4. 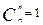 ;
;
5. 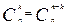 ;
;
6.  .
.
Формула бінома Ньютона
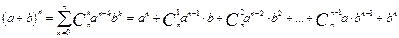 .
.
2. АКСІОМАТИКА ДІЙСНИХ ЧИСЕЛ
Множина  називається множиною дійсних чисел, а її елементи – дійсними числами, якщо вона задовольняє комплексу умов (аксіом) 1-5:
називається множиною дійсних чисел, а її елементи – дійсними числами, якщо вона задовольняє комплексу умов (аксіом) 1-5:
1. Операція додавання.
Для будь-якої упорядкованої пари 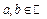 визначено, причому єдиним чином, елемент
визначено, причому єдиним чином, елемент 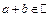 , який називається їхньою сумою так, що при цьому мають місце наступні властивості:
, який називається їхньою сумою так, що при цьому мають місце наступні властивості:
1.1. 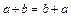

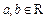 (комутативність).
(комутативність).
1.2. 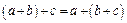

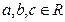 (асоціативність).
(асоціативність).
1.3. В  існує елемент, що позначається
існує елемент, що позначається 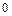 і називається нулем такий, що
і називається нулем такий, що 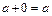

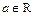 .
.
1.4. Для 
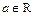 існує елемент з
існує елемент з  , що називається протилежним до
, що називається протилежним до 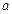 і позначається
і позначається 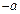 , такий що
, такий що 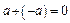 .
.
2. Операція множення.
Для будь-якої упорядкованої пари елементів 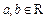 визначено, причому єдиним чином, елемент
визначено, причому єдиним чином, елемент 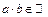 , що називається їхнім добутком так, що при цьому мають місце наступні властивості:
, що називається їхнім добутком так, що при цьому мають місце наступні властивості:
2.1. 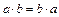

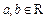 (комутативність).
(комутативність).
2.2. 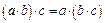

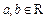 (асоціативність).
(асоціативність).
2.3. В 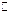 існує елемент, що позначається
існує елемент, що позначається 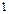 і називається одиницею, такий, що
і називається одиницею, такий, що 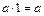

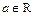 .
.
2.4. 
 ,
, 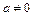 існує елемент з
існує елемент з  , що називається оберненим до
, що називається оберненим до 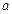 і позначається
і позначається 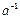 або
або 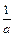 , такий, що
, такий, що 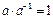 .
.
3. Зв’язок операцій додавання і множення.
3.1. 
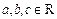
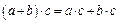 (дистрибутивність множення відносно додавання).
(дистрибутивність множення відносно додавання).
Зауваження. В алгебрі множину, яка задовольняє аксіоми 1-3 називають полем.
4. Аксіома упорядкованості.
Для кожного 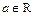 визначено одне з трьох співвідношень:
визначено одне з трьох співвідношень:
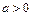 ,
, 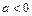 ,
, 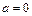 ,
,
причому умови 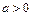 і
і  – еквівалентні, а також, якщо
– еквівалентні, а також, якщо 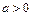 і
і 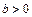 , то
, то 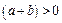 і
і 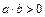 .
.
Аксіома 4 дає можливість порівнювати два елемента із 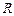 за величиною.
за величиною.
Елемент 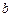 називається більшим за елемент,
називається більшим за елемент, 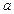 і пишуть
і пишуть 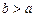 , або, що є те ж саме, елемент
, або, що є те ж саме, елемент 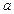 називається меншим за елемент
називається меншим за елемент 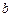 , і пишуть
, і пишуть 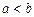 , якщо
, якщо 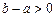 .
.
Для будь-якої упорядкованої пари 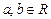 сума
сума 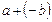 називається різницею
називається різницею 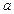 і
і 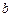 і позначається через
і позначається через 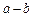 , тобто
, тобто
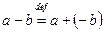 .
.
Для будь-якої упорядкованої пари 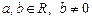 добуток
добуток 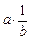 називається часткою від ділення
називається часткою від ділення 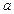 на
на 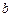 і позначається через
і позначається через 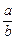 , або
, або 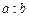 , або
, або 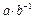 , тобто
, тобто
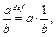
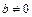 .
.
5. Аксіома неперервності.
Якими б не були непорожні множини 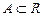 і
і 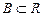 , у яких
, у яких 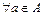 і
і 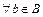 виконується нерівність
виконується нерівність 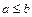 , існує такий елемент
, існує такий елемент 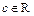 , що для будь-яких
, що для будь-яких 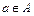 і
і 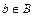 виконуються нерівністі
виконуються нерівністі 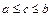 .
.
Теорема. Множина  , що задовольняє аксіомам 1-5, існує і єдина з точністю до ізоморфізму, що зберігає порядок. Тобто, якщо
, що задовольняє аксіомам 1-5, існує і єдина з точністю до ізоморфізму, що зберігає порядок. Тобто, якщо  і
і 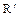 – дві множини, які задовольняють аксіомам 1-5, то знайдеться бієкція
– дві множини, які задовольняють аксіомам 1-5, то знайдеться бієкція 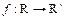 , яка задовольняє умовам:
, яка задовольняє умовам:
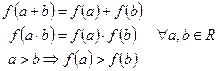
2.1. Наслідки із аксіом
2.1.1. Властивості операцій додавання і множення
10. Є диність нуля (тільки одне число з  має властивість нуля).
має властивість нуля).
20. Єдиність одиниці.
30. Єдиність протилежного елемента.
40. Єдиність оберненого елемента.
50. 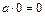

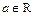 .
.
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 803; Нарушение авторских прав?; Мы поможем в написании вашей работы!