Доведення. 1) Доведемо єдиність нуля

1) Доведемо єдиність нуля.

Припустимо, що крім нуля 0 існує ще один нуль 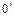. Тоді в силу 1.3 маємо 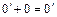і 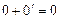. Згідно комутативності (1.1) ліві частини цих рівностей дорівнюють одна одній. Звідси випливає, що .

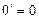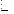
2) Доведемо єдиність одиниці.

Нехай крім одиниці 1 існує ще одна одиниця 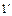. Перемножимо: 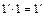. З іншого боку: .

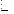
3) Доведемо єдиність протилежного елемента.

Припустимо, що крім 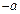число 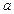має ще одне протилежне число 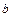, тобто

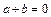і .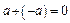

Очевидно,

. (*)

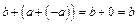З іншого боку,

(**)

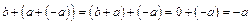Із (*) і (**) випливає що .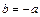

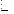
5) Доведемо .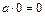

За означенням різниці 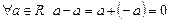. Тоді

.

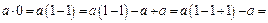
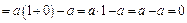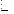
2.1.2. Властивості упорядкованості

1⁰. Якщ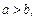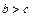о , то .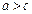

2⁰. Якщ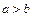о , то .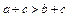

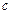
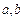
3⁰. виконується одне з трьох співвідношень

, , .

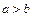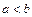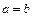4⁰. Якщ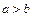о , то .

5⁰. Якщо , то .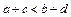

6⁰. Якщ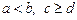о , то .

7⁰. Якщ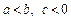о , то .

8⁰. .

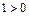2.2. Зображення дійсних чисел у вигляді точок прямої

Розглянемо пряму з вказаним напрямком. Виявляється, що існує бієкція із на цю пряму, при якій число 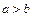зображається точкою, що лежить праворуч від точки, яка зображає число .

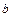2.3. Абсолютна величина (модуль) дійсного числа

За означенням , .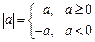

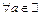Властивості модуля

1⁰. ;

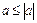2⁰. , ;

3⁰. ;

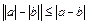4⁰. .

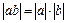2.4. Розширена числова пряма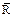

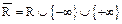– розширена множина дійсних чисел (розширена числова пряма).

За означенням приймають:

;

;

;

;

;

;

;

;

;

;

.

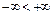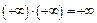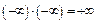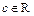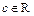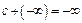
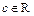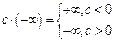Невизначеності: , , .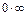

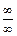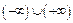2.4.1. Околи на розширеній числовій прямій

1. Нехай , .

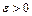Означення. 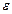- околом точки 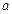називається множина точок 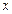числової прямої, що задовольняють нерівності .

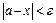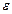-окіл точки 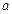позначається .

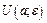радіус околу. 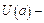окіл точки 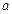деякого радіуса.

2. Означення. Околом невласної точки 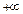називається будь-яка множина виду:

, де 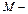будь-яке число.

3. Означення. Околом невласної точки 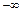називається будь-яка множина виду:

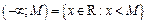, де 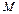– будь-яке число.

4. Означення. Околом невласної точки 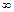називається будь-яка множина виду:

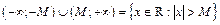, де .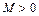

2.5. Обмежені і необмежені множини. Верхня і нижня межі

Означення. Множина 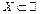називається обмеженою зверху, якщо 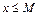, . Число 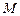називається верхньою межею множини .

Множина обмежена зверху, якщо вона міститься в деякому околі точки . Верхніх меж у обмеженої зверху множини нескінченно багато.

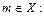
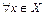Означення. Нехай є обмежена зверху множина. Якщо існує , то 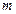називається максимальним елементом множини ,

.

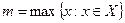Означення. Множина 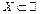називається обмеженою знизу, якщо .

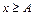
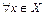Число називається нижньою межею множини .

лежить в деякому околі точки 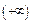. Нижніх меж у обмеженої знизу множини нескінченно багато.

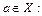
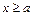
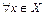Означення. Нехай обмежена знизу множина. Якщо існує , то 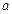називається мінімальним елементом множини ,

.

Означення. Множина 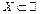називається обмеженою, якщо вона одночасно обмежена знизу і зверху, тобто .

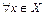Множина обмежена, якщо .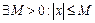

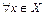Множина лежить в деякому околі нуля.

Означення. Множина 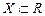необмежена зверху, якщо для .

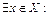
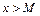Означення. Множина 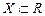необмежена знизу, якщо для .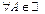

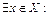
2.6. Точна верхня і точна нижня межі множини

Означення. Нехай – обмежена зверху множина. Її точною верхньою межею називається мінімальний елемент у множині її верхніх меж.

Нехай – обмежена зверху множина. Число 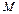– точна верхня межа множини , якщо:

1) 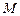– верхня межа ;

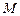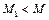2) будь-яке число менше за не є верхньою межею , тобто якщо , то .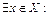

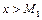Позначення: (sup - supremum).

Означення. Нехай – обмежена знизу множина. Її точною нижньою межею називають максимальний елемент у множині її нижніх меж.

Нехай – обмежена знизу множина. Число – точна нижня межа множини , якщо:

1) – нижня межа ;

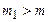2) будь-яке число більше за не є нижньою межею , тобто якщо , то .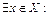

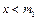Позначення: 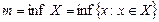(inf - infimum).

Теорема 1 (про існування точної верхньої межі). Нехай 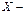обмежена зверху множина. Тоді її точна верхня межа існує.

Дата добавления: 2014-11-20