Доведення. Теорема про граничну точку

Теорема про граничну точку

Означення. Нехай дано деяку множину 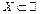. Будемо говорити, що точка 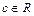є граничною точкою , якщо в будь-якому околі точки 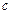міститься хоча б одна точка множини , відмінна від .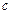

Або інакше:

точка 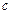називається граничною точкою множини , якщо в будь-якому околі 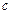міститься нескінченно багато точок із .

Теорема. Будь-яка обмежена нескінченна множина точок має хоча б одну граничну точку.

Нехай – вихідна множина точок. Вона обмежена, отже, міститься в деякому відрізку .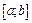

Припустимо супротивне, тобто ніяка точка з 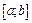не є граничною для (якщо має граничні точки, то вони обов’язково містяться в 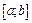). Це означає, що для кожної точки 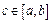знайдеться окіл 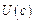, що містить не більше ніж скінченну множину точок із . Об’єднання всіх околів 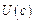містить відрізок 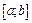, тобто .

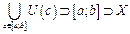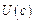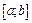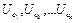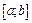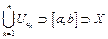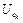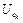За попередньою теоремою: із нескінченної системи інтервалів , що покривають , можна виділити скінченну підсистему , яка також покриває відрізок , тобто . І оскільки, в кожному інтервалі міститься не більше, ніж скінченна множина точок із , то і в об’єднанні міститься скінченна множина точок із , тоді і сама множина містить скінченне число точок.

Таким чином, ми одержали суперечність, оскільки в за умовою міститься нескінченна множина точок. Значить, знайдеться хоча б одна гранична точка множини .

3. ГРАНИЦЯ ЧИСЛОВОЇ ПОСЛІДОВНОСТІ

Означення. Точка 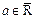називається границею числової послідовності 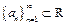, якщо в будь-якому околі точки 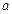містяться всі члени цієї послідовності, починаючи з деякого номера.

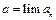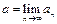Позначення: , або , або .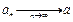

Очевидно, точка 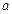є границею послідовності 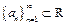, якщо поза будь-яким околом точки 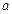міститься лише скінченна кількість членів цієї послідовності.

Розглянемо чотири випадки.

1. 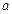– скінченне число.

,

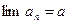
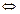
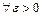
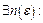
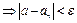(всі )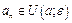

2.

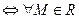
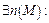
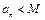
3.

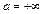
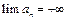
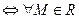
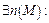
4.

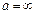
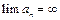
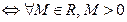
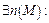
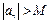
Означення. Якщо границя 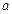послідовності 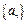скінченне число, то послідовність називається збіжною, або говорять, що послідовність збігається.

Означення. Послідовність, границя якої дорівнює 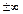або 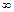, називається нескінченно великою.

Означення. Послідовність, що збігається до нуля, називається нескінченно малою.

3.1. Теореми про границі

Теорема 1. Збіжна послідовність має тільки одну границю.

Дата добавления: 2014-11-20