Мультиколлинеарность

Мультиколлинеарность это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. При наличии мультиколлинеарности МНК-оценки формально существуют, но обладают рядом недостатков:

1) Небольшое изменение исходных данных приводит к существенному изменению оценок регрессии;

2) оценки, как правило, имеют большие стандартные ошибки, малую значимость, в то время как модель в целом является значимой (высокое значение ).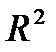

Если при оценке уравнения регрессии несколько факторов оказались незначимыми, то нужно выяснить, нет ли среди них сильно коррелированных между собой. При наличии мультиколлинеарности для ее устранения или уменьшения имеется ряд методов, в частности пошаговые процедуры отбора наиболее информативных переменных. Например, на первом шаге рассматривается лишь одна объясняющая переменная, имеющая с зависимой переменной Y наибольший коэффициент детерминации. На втором шаге включается в регрессию новая объясняющая переменная, которая вместе с первоначально отобранной образует пару объясняющих переменных, имеющую с Y наиболее высокий (скорректированный) коэффициент детерминации. На третьем шаге вводится в регрессию еще одна объясняющая переменная, которая вместе с двумя первоначально отобранными образует тройку объясняющих переменных, имеющую с Y наибольший (скорректированный) коэффициент детерминации, и т.д. Процедура введения новых переменных продолжается до тех пор, пока будет увеличиваться соответствующий (скорректированный) коэффициент детерминации 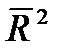. В большинстве случаев получаемые с помощью пошаговой процедуры наборы переменных оказываются оптимальными или близкими к оптимальным.

Пример. Используя данные Федеральной службы государственной статистики России (за двенадцать месяцев) требуется:

1) Оценить влияние факторов (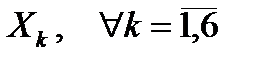) на изучаемый показатель (Y) и друг на друга с помощью коэффициентов линейной корреляции.

2) Используя процедуру выбора факторов, предложить и построить подходящую линейную регрессионную модель изучаемого показателя.

3) Дать экономическую интерпретацию с использованием коэффициентов эластичности. Получить точечные и интервальные прогнозы изучаемого показателя на следующий месяц.

в % к предыдущему периоду	Оборот розничной торговли непродовольствен-ными товарами	Располагаемые денежные доходы	Реальная заработная плата	Индексы цен товаров и услуг населению	Индексы цен продовольственных товаров	Индексы цен непродовольственных товаров	Индексы цен платных услуг населению
	Y	X1	X2	X3	X4	X5	X6
Июнь	100,6	107,4	106,5	100,6	100,7	100,3	100,9
Июль	102,9	100,3	99,5	100,5	100,3	100,4	100,9
Август	104,4		100,6	99,9		100,5	100,8
Сентябрь	101,3	106,8	102,2	100,3	99,3	101,1	100,9
Октябрь	103,8	99,1	98,2	100,6	100,4	100,7	100,7
Ноябрь	100,8	101,8	101,8	100,7	100,9	100,6	100,6
Декабрь	117,3		125,7	100,8	101,1	100,5	100,8
Январь 2006г.	75,2	52,1	76,8	102,4	102,0	100,4	106,2
Февраль	100,4	121,9		101,7	103,0	100,5	101,0
Март	109,9	108,9	106,2	100,8	101,2	100,4	100,7
Апрель		105,5		100,4	100,3	100,3	100,6
Май		99,1	103,7	100,5	100,5	100,4	100,6

Построим линейную регрессионную модель с использованием всех шести объясняющих переменных с помощью функции Регрессия (заметим, что во входной интервал X следует вводить сразу весь набор значений объясняющих переменных):

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,964746
R-квадрат	0,930735
Нормированный R-квадрат	0,847618
Стандартная ошибка	3,785404
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		962,7403	160,4567	11,19782	0,00898589
Остаток		71,6464	14,32928
Итого		1034,387

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	635,5103686	684,2110492	0,928822137	0,395611	-1123,31	2394,331
X1	0,131664673	0,239250121	0,550322286	0,605779	-0,48335	0,746677
X2	0,4591524	0,377586527	1,216019024	0,27825	-0,51146	1,429769
X3	53,11332128	67,25470889	0,789733866	0,465468	-119,77	225,9971
X4	-24,01925153	28,81047116	-0,83369867	0,442444	-98,078	50,04042
X5	-21,09145229	24,61310441	-0,85691962	0,430635	-84,361	42,17855
X6	-13,901573	15,58480592	-0,89199525	0,413259	-53,963	26,16045

Анализируя выходные данные, приходим к выводу, что все коэффициенты регрессии незначимы при уровне значимости 0,05 (все Р -значения больше 0,05). С другой стороны, высокое значение 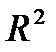и значимость уравнения в целом (F -значение, равное 0,008986, меньше 0,05), указывают на то, что в модели присутствуют значимые переменные.

1) Для отбора факторов в модель регрессии и оценки их мультиколлинеарности, найдем матрицу парных коэффициентов корреляции. Расчет корреляционной матрицы предусмотрен функцией Корреляция в пакете Анализ данных. Для вызова функции Корреляция необходимо выбрать команду меню Данные → Анализ данных. На экране раскроется диалоговое окно Анализ данных, в котором следует выбрать значение Корреляция. Тогда на экране появится диалоговое окно Корреляция, представленное на рис. 12.

Во входной интервал вводим числовые данные всех переменных модели вместе с буквами, не забыв поставить флажок на метку. Задав выходной интервал (или оставив по умолчанию новый рабочий лист), получим матрицу парных коэффициентов корреляции:

	Y	X1	X2	X3	X4	X5	X6
Y
X1	0,896244
X2	0,913353	0,929783
X3	-0,65744	-0,41067	-0,49785
X4	-0,2807	0,014257	-0,1398	0,852351
X5	0,079024	0,074599	0,045947	-0,21036	0,38206
X6	-0,8566	-0,76876	-0,72354	0,801879	0,38871	0,12163

Анализируя вышеуказанную матрицу, замечаем, что наиболее существенное влияние на фактор Y оказывают переменные X2

(), X1 (), X6 (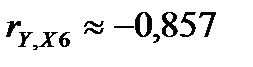). Кроме этого, существует тесная корреляционная связь между переменными X1 и X2

(), X3 и X6 (), X3 и X4 (). Поэтому при построении регрессии с использованием всех объясняющих переменных будет иметь место мультиколлинеарность. Для устранения мультиколлинеарности применим процедуру пошагового отбора наиболее информативных переменных.

2) 1-й шаг. Из объясняющих переменных X1 ‒ X6 выделяется переменная X2, имеющая с зависимой переменной Y наибольший коэффициент детерминации (равный для парной модели квадрату коэффициента корреляции ). Воспользуемся функцией Регрессия для получения парной регрессии с участием переменных Y и X2. Ограничимся при этом выводом Регрессионной статистики:

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,913353
R-квадрат	0,834213
Нормированный R-квадрат	0,817635
Стандартная ошибка	4,141107
Наблюдения

Скорректированный коэффициент детерминации равен 0,818.

2-й шаг. Среди всевозможных пар объясняющих переменных X2, X j, j = 1, 3, 4, 5, 6, выбирается пара (X2, X6), имеющая с зависимой переменной Y наиболее высокий скорректированный коэффициент детерминации, равный 0,896. Результаты расчетов приводятся ниже.

X2,X1			X2,X3			X2,X4
ВЫВОД ИТОГОВ		ВЫВОД ИТОГОВ		ВЫВОД ИТОГОВ
Регрессионная статистика		Регрессионная статистика		Регрессионная статистика
Множественный R	0,922243		Множественный R	0,942792		Множественный R	0,926332
R-квадрат	0,850532		R-квадрат	0,888857		R-квадрат	0,858091
Нормированный R-квадрат	0,817317		Нормированный R-квадрат	0,864158		Нормированный R-квадрат	0,826556
Стандартная ошибка	4,144712		Стандартная ошибка	3,574056		Стандартная ошибка	4,038544
Наблюдения			Наблюдения			Наблюдения

X2,X6			X2,X5
ВЫВОД ИТОГОВ		ВЫВОД ИТОГОВ
Регрессионная статистика		Регрессионная статистика
Множественный R	0,956363		Множественный R	0,914106
R-квадрат	0,91463		R-квадрат	0,835589
Нормированный R-квадрат	0,895659		Нормированный R-квадрат	0,799054
Стандартная ошибка	3,13236		Стандартная ошибка	4,346955
Наблюдения			Наблюдения

3-й шаг. Среди всевозможных троек объясняющих переменных

(X2, X6, X j), j = 1, 3, 4, 5, наиболее информативной оказалась тройка

(X2, X6, X4), имеющая максимальный скорректированный коэффициент детерминации, равный 0,885. Результаты расчетов:

X1,X2,X6			X2,X3,X6
ВЫВОД ИТОГОВ		ВЫВОД ИТОГОВ
Регрессионная статистика		Регрессионная статистика
Множественный R	0,956621		Множественный R	0,957054
R-квадрат	0,915125		R-квадрат	0,915953
Нормированный R-квадрат	0,883296		Нормированный R-квадрат	0,884435
Стандартная ошибка	3,31274		Стандартная ошибка	3,296542
Наблюдения			Наблюдения

X2,X4,X6			X2,X5,X6
ВЫВОД ИТОГОВ		ВЫВОД ИТОГОВ
Регрессионная статистика		Регрессионная статистика
Множественный R	0,957151		Множественный R	0,956363
R-квадрат	0,916138		R-квадрат	0,914631
Нормированный R-квадрат	0,884689		Нормированный R-квадрат	0,882618
Стандартная ошибка	3,292908		Стандартная ошибка	3,322358
Наблюдения			Наблюдения

Так как скорректированный коэффициент детерминации на 3-м шаге не увеличился, то в регрессионной модели достаточно ограничиться лишь двумя отобранными ранее объясняющими переменными X2 и X6. Построим эту линейную регрессионную модель с помощью функции Регрессия:

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,956363154
R-квадрат	0,914630482
Нормированный R-квадрат	0,895659478
Стандартная ошибка	3,132359619
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		946,0816	473,0408	48,21202	1,55E-05
Остаток		88,30509	9,811677
Итого		1034,387

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	302,8787507	98,34281602	3,079825888	0,013144	80,41184	525,3457
X2	0,556121622	0,127354024	4,36673772	0,001806	0,268027	0,844216
X6	-2,547239382	0,874833084	-2,91168615	0,017264	-4,52625	-0,56823

Оцененное уравнение имеет вид:

.

Нетрудно убедиться в том, что теперь все коэффициенты регрессии значимы при уровне значимости 0,05 (все Р -значения меньше 0,05).

Кроме рассмотренной выше пошаговой процедуры присоединения объясняющих переменных используются также пошаговые процедуры присоединения ‒ удаления и процедура удаления объясняющих переменных, изложенные, например, в [5]. Следует отметить, что какая бы пошаговая процедура ни использовалась, она не гарантирует определения оптимального (в смысле получения максимального коэффициента детерминации) набора объясняющих переменных. Однако в большинстве случаев получаемые с помощью пошаговых процедур наборы переменных оказываются оптимальными или близкими к оптимальным.

3) Дадим экономическую интерпретацию найденного уравнения с использованием коэффициентов эластичности.

Согласно формулам (2.2) 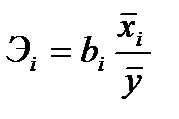. По условию 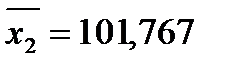, , . Тогда ; .

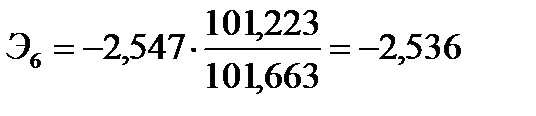Коэффициент означает, что при увеличении реальной заработной платы на 1% оборот розничной торговли непродовольственными товарами вырастет в среднем на 0,557%. Коэффициент означает, что при увеличении индексов цен платных услуг населению на 1% оборот розничной торговли непродовольственными товарами упадет в среднем на 2,536%.

Получим теперь точечные и интервальные прогнозы изучаемого показателя на следующий месяц, если реальная заработная плата в июне предполагается на уровне 108%, а индексы цен платных услуг населению на уровне 100,7% по отношению к майским показателям. Подставив указанные значения в полученное уравнение, получим точечную оценку среднего оборота розничной торговли непродовольственными товарами в июне:

.

Для построения интервальной оценки изучаемого показателя воспользуемся формулой (2.1). Для наглядности приведем ряд промежуточных результатов:

; ; ;

; .

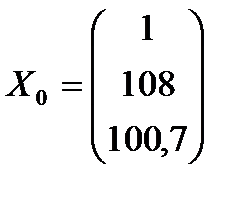При расчетах были использован математические функции пакета Мастера функций Excel (категория математические) МУМНОЖ (возвращает матричное произведение двух массивов) и МОБР (возвращает обратную матрицу). В результате вычислений имеем: . Из таблиц критических точек распределения Стьюдента (см. также Excel ‒ f_x ‒ статистические ‒ стьюдент.обр.2х) находим: 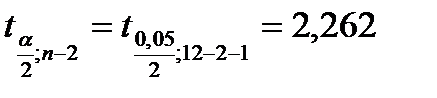. Подставив эти значения в формулу (2.1), получим 95%-ный доверительный интервал для прогнозного среднего значения результативного признака Y при X₂ = 108, X₆ = 100,7:

,

.

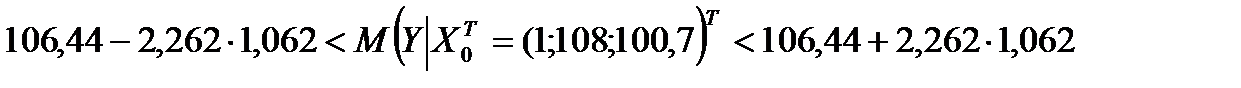Основываясь на выборочных данных можно утверждать, что средний оборот розничной торговли непродовольственными товарами в июне будет находится в найденном доверительном интервале с вероятностью 0,95.

Примерные варианты контрольной работы

Вариант 1

1. Верно ли, что коэффициент b регрессии Y на X имеет тот же знак, что и коэффициент корреляции 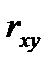? Почему?

2. По месячным данным за 6 лет была построена следующая регрессия:

= − 12,23 + 0,91 · DINC – 2,1 · SR, = 0,976

t = (−3,38) (123,7) (−3,2)

Здесь Y – потребление, DINC – располагаемый доход, SR – процентная банковская ставка по вкладам, t ‒ соответствующие значения t-статистики. Есть ли основания считать, что практически весь доход уходит на потребление?

3. В таблице приведены данные о величине личного дохода (PI) и потребительские расходы населения США на телефон (TELE) за период 1959 – 1970 гг. Все данные приводятся в миллиардах долларов в ценах 1972 г.

Годы
PI	544,9	559,7	575,4		622,9		700,4	740,6	774,4	816,2	853,5	876,8
TELE	4,7	5,0	5,4	5,7	6,1	6,6	7,3	8,1	8,7	9,5	10,4	11,2

1) оценить по МНК коэффициенты линейной регрессии Y = + X + U;

2) дать экономическое толкование построенной регрессии;

3) вычислить коэффициент детерминации R , сделать соответствующие выводы;

4) сделать прогноз расходов на телефон на 1972 г, если уровень доходов предполагается на уровне 951,4.

5) рассчитать доверительный интервал для среднего значения Y с вероятностью 95%.

Вариант 2

1. Чем скорректированный коэффициент детерминации отличается от обычного?

2. Эмпирическое уравнение зависимости объема S сбережений домохозяйства от располагаемого дохода Y в предыдущем году и от величины Z процентной ставки в рассматриваемом году (данные за 10 лет) имеет вид: s = 2, 96 + 0,124 y 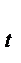+ 3,55 z , причем = 176,4; 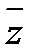= 3,36; = 36,8.

1) найти коэффициенты эластичности;

2) дать экономическую интерпретацию.

3. В следующей таблице приведены данные по реальному ВНП (GNP), реальному объему потребления (CONG) и объему инвестиций (INV) для некоторой страны.

GNP
CONG
INV	38,2	41,9	46,5	52,1	48,1	38,3	45,4	52,1	56,8	57,5

GNP
CONG
INV	50,9	54,5	44,7	50,4	65,8	63,7		76,4	71,6	71,8

а) Постройте уравнение регрессии .

б) Оцените качество построенного уравнения.

в) Имеет ли место мультиколлинеарность для построенного вами уравнения?

г) Если мультиколлинеарность присутствует, то, найти наилучшую по качеству линейную регрессионную модель, исключив при этом мультиколлинеарность.

Литература

1. Бородич С. А. Вводный курс эконометрики: Учебное пособие ‒ Мн.: БГУ, 2000. ‒ 354 с.

2. Новиков А. И. Эконометрика: Учебное пособие. ‒ М.: ИНФРА-М, 2003. ‒ 106 с.

3. Кремер Н. Ш., Путко Б. А. Эконометрика: Учебник для вузов / Под ред. проф. Н. Ш. Кремера. ‒ М.: ЮНИТИ-ДАНА, 2002. ‒ 311 с.

4. Доугерти К. Введение в эконометрику: Пер. с англ. ‒ М.:

ИНФРА-М, 1997.

5. Айвазян С. А., Мхитарян В. С. Прикладная статистика и основы эконометрики. ‒ М.: ЮНИТИ, 1998.

6. Эконометрика / Под ред. Н. И. Елисеевой. ‒ М.: Финансы и статистика, 2001.

7. Практикум по эконометрике: Учеб. пособие / И. И. Елисеева,

С. В. Курышева, Н. М. Гордеенко и др.; Под ред. И. И Елисеевой. ‒ М.: Финансы и статистика, 2005. ‒ 192 с.

8. Эконометрика. Курс лекций. ‒ Учебно-методическое пособие. Составители: А. Т. Козинова, А. А. Отделкина. ‒ Н. Новгород, 2004 ‒ 95 с.

Оглавление

Глава 1 Парная линейная регрессия ……………………………..………5

1.1. Взаимосвязи экономических переменных……………………………...5

1.2. Метод наименьших квадратов…………………………...……………...8

1.3. Предпосылки регрессионного анализа…………...……………………11

1.4. Расчет стандартных ошибок коэффициентов регрессии……………..14

1.5 Проверка гипотез относительно коэффициентов регрессии………....16

1.6 Проверка общего качества уравнения регрессии…………………......19

1.7 Доверительные интервалы для зависимой переменной……………...21

1.8 Реализация типовых задач в MS Excel………………………………...23

Глава 2 Множественная линейная регрессия…………… …………….30

2.1 Определение параметров уравнения регрессии……..………………...30

2.2 Интервальные оценки коэффициентов теоретического уравнения регрессии и зависимой переменной………………………….……………...32

2.3 Анализ качества выборочного уравнения множественной линейной регрессии………………………………………………………………….…...33

2.4 Мультиколлинеарность………………………………………………....35

2.4 Примерные варианты контрольной работы……………………….......43

Литература ……………………………………………………………………45

© Нижегородский государственный архитектурно-

строительный университет, 2014

Любимцев Олег Владимирович

Любимцева Ольга Львовна

Дата добавления: 2014-11-20