Указания к выполнению контрольной работы 4 страница

3) методом экстраполяции определить прогноз экономического показателя на 2002 и 2003 г.г.;

4) начертить графики первичного и выроненного рядов.

10.1.

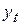
	167,6	165,8	167,4	168,0	167,5	167,2	166,5	166,5	166,4

10.2.

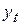
	169,1	167,3	168,9	169,5	169,0	168,7	168,0	168,0	167,9

10.3.

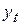
	166,1	164,3	165,9	166,5	166,0	165,7	165,0	165,0	164,9

10.4.

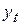
	168,6	166,8	168,4	169,0	168,5	168,2	167,5	167,5	167,4

10.5.

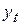
	166,6	164,8	166,4	167,0	166,5	166,2	165,5	165,5	165,4

10.6.

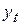
	168,1	166,3	167,9	168,5	168,0	167,7	167,0	167,0	166,9

10.7.

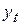
	170,1	168,3	169,9	170,5	170,0	169,7	169,0	169,0	168,9

10.8.

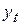
	165,6	163,8	165,4	166,0	165,5	165,2	164,5	164,5	164,4

10.9.

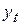
	169,6	167,8	169,4	170,0	169,5	169,2	168,5	168,5	168,4

10.10.

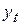
	169,1	167,3	168,9	169,5	169,0	168,7	168,0	168,0	167,9

Методические указания к выполнению контрольной работы.

Решение типовых задач.

Задача 1.

Из генеральной совокупности 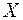, распределенной по нормальному закону, извлечена выборка. Требуется:

1. Составить вариационный, статистический и выборочный ряды распределения; найти размах выборки;

По полученному распределению выборки:

2. Построить полигон относительных частот;

3. Построить график эмпирической функции распределения;

4. Вычислить выборочную среднюю, выборочную дисперсию, выборочное исправленное среднее квадратическое отклонение, моду и медиану;

5. С надежностью найти доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения изучаемого признака генеральной совокупности.

1.0.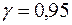

5,6	5,8	5,0	5,4	5,2	5,8	5,2	5,6
5,6	5,6	5,4	5,0	5,4	5,8	5,4	5,6
5,4	5,2	5,4	5,4	5,6	5,0	6,0	5,8
5,2	5,8	5,6	5,8	6,0	5,2	5,8	6,0
6,2	5,4	6,2	5,6	6,0	5,6	5,2	5,6

Составим вариационный ряд. Напомним, что вариационным рядом называется последовательность наблюдаемых значений признака 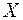, расположенных в неубывающем порядке , ,…, , где … . Следовательно, в нашей задаче вариационный ряд запишется так:

5,0	5,0	5,0	5,2	5,2	5,2	5,2	5,2
5,2	5,4	5,4	5,4	5,4	5,4	5,4	5,4
5,4	5,6	5,6	5,6	5,6	5,6	5,6	5,6
5,6	5,6	5,6	5,8	5,8	5,8	5,8	5,8
5,8	5,8	6,0	6,0	6,0	6,0	6,2	6,2

Составим статистический ряд распределения данной нам выборки

	5,0	5,2	5,4	5,6	5,8	6,0	6,2

- варианты, - частоты.

Найдем объем выборки

.

Относительная частота вычисляется по формуле .

Запишем выборочный ряд распределения

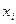
	5,0	5,2	5,4	5,6	5,8	6,0	6,2

.

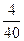
Размах выборки , т.е. в нашем случае .

Построим полигон относительных частот

Вычислим выборочную среднюю

= = ()= =5,56.

Построим график эмпирической функции распределения 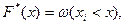где ( число вариант, меньших, чем значение аргумента ).

Вычислим выборочную дисперсию , где в нашем случае = ()= =31,012

.

Найдем выборочное среднее квадратическое отклонение

Вычислим "исправленную" дисперсию , которая выражается формулой

(в нашем случае )

и "исправленное" среднее квадратическое отклонение .

Модой называется варианта с наибольшей частотой, т.е. в нашей задаче . Медиана 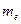- варианта, которая делит вариационный ряд на две части, равные по числу вариант, т.е. в нашей задаче .

Найдем с надежностью g=0,95 доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения изучаемого признака генеральной совокупности.

Так как по условию задачи генеральная совокупность xраспределена по нормальному закону и объем выборки равен n=40, то искомый доверительный интервал для оценки математического ожидания имеет вид

,

где - среднее квадратическое отклонение, а величина t определяется по таблице значений функции Лапласа из равенства .

Следовательно, в нашем случае последнее равенство принимает вид . Из этого равенства по таблице значений интегральной функции Лапласа находим значение t=1,96. Величина была найдена ранее: и .

Вычислим . .

Учитывая, что , доверительный интервал для оценки математического ожидания запишется или, окончательно, .

Доверительный интервал для среднего квадратического отклонения нормально распределенной случайной величины находится по формуле , где s - "исправленное" среднее квадратическое отклонение, а d находится по формуле , где величина q определяется по специальной таблице значений функции .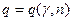

Найдем для нашей конкретной задачи:

q=q(0,95;40)=0,24; d=sq=0,321×0,24=0,077. Следовательно, или окончательно .

На этом решение задачи 1 закончено.

Задача 2.

Для выборки, извлеченной из генеральной совокупности и представленной интервальным рядом (в первой строке указаны интервалы значений исследуемого количественного признака X генеральной совокупности; во второй – частоты , т.е. количество элементов выборки, значения признака которых принадлежат указанному интервалу), требуется:

1) Построить полигон относительных накопленных частот (кумулятивную кривую);

2) Построить гистограмму частот и гистограмму относительных частот;

3) Найти выборочную среднюю, выборочную дисперсию, моду и медиану;

4) Проверить на уровне значимости гипотезу о нормальном распределении признака 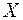генеральной совокупности по критерию согласия Пирсона;

5) В случае согласованности с нормальным распределением найти с надежностью 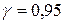доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака 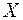генеральной совокупности.

2.0.

	3-5	5-7	7-9	9-11	11-13	13-15	15-17

.

В нашем случае n=2750.Тогда на основе данной таблицы построим интервальный статистический и интервальный выборочный ряды распределения, сведенные в одну таблицу.

i
	3-5	5-7	7-9	9-11	11-13	13-15	15-17
	0,0036	0,0255	0,1636	0,3527	0,3127	0,12	0,0218
	0,0036	0,0291	0,1927	0,5454	0,8581	0,9781

Построим полигон относительных накопленных частот (кумулятивную кривую);

Построим гистограмму частот.

В нашем случае исследуемый признак X может принимать значения на отрезке [3;17]. Интервальная группировка выполнена таким образом, что длина каждого интервала равна h=2. Площадь прямоугольника, построенного на i-ом интервале, должна равняться . Это значит, что высота i-го прямоугольника будет .

На остальных интервалах прямоугольники строятся аналогично.

Если высоту i-го прямоугольника определим как , то получим гистограмму относительных частот, которую можно рассматривать как аналог дифференциальной функции распределения в теории вероятностей.

Для того, чтобы найти выборочную среднюю, воспользуемся формулой

, где k - количество интервалов, n - объем выборки.

.

Для вычисления выборочной дисперсии воспользуемся формулой . В случае интервальной группировки находится по формуле

= .

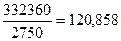Теперьможно окончательно вычислитьвыборочную дисперсию

.

Найдем выборочное среднее квадратическое отклонение

.

Отыщем выборочный коэффициент вариации

.

Найденное значение выборочного коэффициента вариации дает наглядное представление о степени относительного рассеяния исследуемого признака.

Отыщем значения "исправленной" дисперсии и "исправленного" среднего квадратического отклонения , .

Для отыскания моды в случае интервальной группировки используем формулу , где - левая граница интервала, имеющего наибольшую интервальную частоту, h - шаг (длина интервала группировки), , R - размах выборки, k - количество интервалов, - наибольшая интервальная частота, - интервальная частота интервала, расположенного слева от интервала с наибольшей интервальной частотой, - интервальная частота интервала, расположенного справа от интервала с наибольшей интервальной частотой.

В нашем случае .

Значение медианы 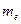для случая интервальной группировки отыщем по формуле 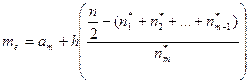, где - левая граница интервала, содержащего медиану, n - объем выборки, h - шаг, - интервальная частота интервала, содержащего медиану, - интервальные частоты всех интервалов, расположенных слева от интервала, содержащего медиану.

Найдем значение медианы 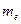для нашей конкретной задачи.

Далее начнем суммировать интервальные частоты слева направо до тех пор пока сумма интервальных частот не превзойдет .Номер последней прибавленной частоты будет совпадать с номером интервала, содержащего медиану распределения: 10+70+450+970=1500>1375. Следовательно, =9, .

Проверим на уровне значимости a=0,05 гипотезу 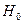о нормальном распределении признака x генеральной совокупности по критерию согласия Пирсона.

Для нашей задачи все условия применимости метода Пирсона выполняются: , для любого интервала .

Проверка гипотезы нормальности по критерию Пирсона основана на сравнении эмпирического и гипотетического распределений, точнее, на сравнении эмпирических и гипотетических интервальных частот. Мера близости между ними оценивается статистикой Пирсона:

, где - интервальные (эмпирические) частоты, - интервальные теоретические частоты, - теоретические вероятности попадания переменной x в i-ый интервал группировки, , - левая граница i-го интервала, - правая граница i-го интервала.

При этом теоретические вероятности рассчитываются в предположении нормальности распределения случайной величины x по формуле:

, где 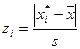и функция есть плотность стандартного нормального распределения, таблица значений которой приведена в приложении 2.

Вычисление наблюдаемого значения статистики Пирсона организуем в форме расчетной таблицы. Для заполнения таблицы нам понадобятся величины , , .

i
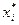
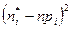
	(3;5)			6,785	3,182	0,0025	0,0023	6,325	3,675	13,506	2,135
	(5;7)			4,785	2,244	0,0325	0,0305	83,87	-13,87	192,516	2,295
	(7;9)			2,785	1,306	0,1691	0,1586	436,15	13,85	191,823	0,440
	(9;11)			0,785	0,368	0,3726	0,3495	961,12	8,875	78,766	0,082
	(11;13)			1,215	0,570	0,3391	0,3181	874,78	-14,78	218,301	0,250
	(13;15)			3,215	1,508	0,1276	0,1197	329,18	0,825	0,681	0,002
	(15;17)			5,215	2,446	0,0198	0,0186	51,15	8,85	78,322	1,531
							0,9973				6,735

Дата добавления: 2014-12-08