
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Указания к выполнению контрольной работы 5 страница
|
|
|
|
Следовательно, 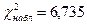 . Заданный уровень значимости
. Заданный уровень значимости 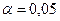 , количество интервалов группировки
, количество интервалов группировки 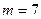 , и потому p=1-a =0,95 и число степеней свободы k=m- 3=4.
, и потому p=1-a =0,95 и число степеней свободы k=m- 3=4.
Теперь по таблице критических точек распределения  отыщем значение
отыщем значение  .
.
Сравним значения 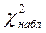 и
и 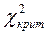 . Имеем 6,735<9,5, следовательно,
. Имеем 6,735<9,5, следовательно, 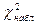 <
<  . Поэтому гипотезу о нормальном распределении признака x принимаем. В этом случае необходимо найти с надежностью g=0,95 доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака x генеральной совокупности. Пример нахождения доверительных интервалов разобран при решении задачи 1 (пятый вопрос).
. Поэтому гипотезу о нормальном распределении признака x принимаем. В этом случае необходимо найти с надежностью g=0,95 доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака x генеральной совокупности. Пример нахождения доверительных интервалов разобран при решении задачи 1 (пятый вопрос).
Таким образом, решение задачи 2 полностью разобрано.
Задача 3.
Проведите сравнительный анализ результатов педагогического эксперимента в контрольных и экспериментальных группах, используя критерий однородности Пирсона.
 , где
, где  и
и 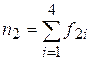 .
.
Уровень значимости положите 
3.0.
Значение варианты 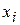
|  2 2
| 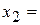 3 3
| 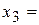 4 4
|  5 5
|
Частота появления 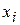 в экспериментальной группе в экспериментальной группе
|  27 27
| 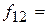 25 25
| 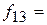 28 28
| 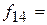 9 9
|
Частота появления 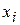 в контрольной группе в контрольной группе
|  9 9
|  5 5
|  18 18
| 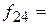 10 10
|
Проведем сравнительный анализ результатов педагогического эксперимента в контрольных и экспериментальных группах, используя критерий однородности Пирсона:
 , где 2, 3, 4, 5 - вариационный ряд (оценки, выставляемые по результатам проведения контрольных работ),
, где 2, 3, 4, 5 - вариационный ряд (оценки, выставляемые по результатам проведения контрольных работ),  - частота появления i-ой варианты в экспериментальной группе,
- частота появления i-ой варианты в экспериментальной группе, 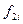 - частота появления i-ой варианты в контрольной группе,
- частота появления i-ой варианты в контрольной группе,  - объем выборки в экспериментальной группе,
- объем выборки в экспериментальной группе,  - объем выборки в контрольной группе, m=4 - количество различных значений варианты (количество интервалов группировки), k=m-1=3 - количество степеней свободы.
- объем выборки в контрольной группе, m=4 - количество различных значений варианты (количество интервалов группировки), k=m-1=3 - количество степеней свободы.
Найдем 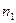 и
и 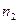 .
.  =27+25+28+9=89,
=27+25+28+9=89,  =9+5+18+10=42.
=9+5+18+10=42.
Теперь вычислим 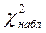 .
.
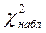 =
= 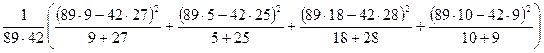 =8,6.
=8,6.
По таблице критических точек распределения  , приведенной в приложении 3, для числа степеней свободы k=3 и уровня значимости a=0,05 находим значение
, приведенной в приложении 3, для числа степеней свободы k=3 и уровня значимости a=0,05 находим значение 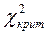 =7,81.
=7,81.
Так как 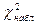 >
>  (8,6>7,81), то согласно правилу принятия решения, делаем вывод, что существуют достоверные различия между результатами проведения контрольных работ в экспериментальной и контрольной группах на уровне надежности g=1-a=1-0,05=0,95.
(8,6>7,81), то согласно правилу принятия решения, делаем вывод, что существуют достоверные различия между результатами проведения контрольных работ в экспериментальной и контрольной группах на уровне надежности g=1-a=1-0,05=0,95.
На этом решение задачи 3 закончено. Приведенный пример с небольшими изменениями взят из работы [7].
Задача 4.
Исследуется зависимость коэффициента усвоения знаний, выраженного в процентах ( %) от уровня посещаемости занятий (
%) от уровня посещаемости занятий (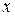 %) в группе из четырнадцати учащихся (
%) в группе из четырнадцати учащихся ( - порядковый номер учащегося). Статистические данные приведены в таблице.
- порядковый номер учащегося). Статистические данные приведены в таблице.
Требуется:
1) Найти оценки параметров линейной регрессии 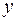 на
на  . Построить диаграмму рассеяния и нанести прямую регрессии на диаграмму рассеяния.
. Построить диаграмму рассеяния и нанести прямую регрессии на диаграмму рассеяния.
2) На уровне значимости  проверить гипотезу о согласии линейной регрессии с результатами наблюдений.
проверить гипотезу о согласии линейной регрессии с результатами наблюдений.
3) С надежностью 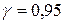 найти доверительные интервалы для параметров линейной регрессии.
найти доверительные интервалы для параметров линейной регрессии.
4.0.

| ||||||||||||||
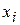
| ||||||||||||||
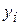
|
Найдем точечные статистические оценки  и
и 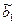 параметров
параметров 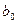 и
и  линейной регрессии Y на X:
линейной регрессии Y на X:  .
.
Для уравнения прямой регрессии  по статистическим данным таблицы 4.0 найдем оценки
по статистическим данным таблицы 4.0 найдем оценки  и
и 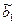 ее параметров методом наименьших квадратов. Применим известные формулы
ее параметров методом наименьших квадратов. Применим известные формулы
 , где
, где 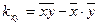 ,
,  ;
;

Вычисления 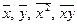 организуем в форме следующей расчетной таблицы:
организуем в форме следующей расчетной таблицы:
| i | 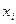
| 
| 
| 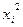
| 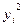
|
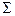
| |||||

| 50,714 | 34,143 | 1836,071 | 2764,286 | 1226,286 |
Таким образом,  ,
,  ,
,  ,
, 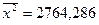 ,
,  .
.
Далее вычисляем ковариации
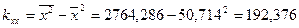 ;
;
 ;
;
 ;
;
и по указанным выше формулам находим
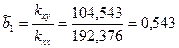 ;
;  .
.
В результате получаем уравнение прямой регрессии
 .
.
Проверим согласованность выбранной линейной регрессии с результатами наблюдений. Для этого решим следующую задачу проверки статистической гипотезы.
На заданном уровне значимости  выдвигается гипотеза
выдвигается гипотеза  об отсутствии линейной статистической связи. Для проверки выдвинутой гипотезы используется коэффициент детерминации
об отсутствии линейной статистической связи. Для проверки выдвинутой гипотезы используется коэффициент детерминации 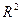 и применяется статистика Фишера F.
и применяется статистика Фишера F.
В случае парной линейной регрессии коэффициент детерминации 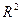 равен квадрату выборочного коэффициента корреляции Пирсона, т.е.
равен квадрату выборочного коэффициента корреляции Пирсона, т.е.  .
.
Статистика F выражается формулой  и при условии справедливости гипотезы имеет классическое распределение Фишера с
и при условии справедливости гипотезы имеет классическое распределение Фишера с  и
и 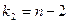 степенями свободы.
степенями свободы.
В соответствии с приведенными формулами вычисляем коэффициент детерминации и наблюдаемое значение статистики Фишера:
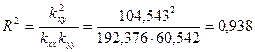 ,
,
 .
.
Критическое значение статистики Фишера 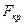 находим по таблице квантилей распределения Фишера, исходя из равенства
находим по таблице квантилей распределения Фишера, исходя из равенства 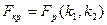 , где p=1-a (порядок квантили),
, где p=1-a (порядок квантили),  и
и 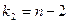 . В данном случае
. В данном случае 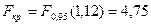 .
.
Сравниваем между собой наблюдаемое и критическое значения статистики Фишера. Так как 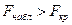 , то выдвинутая гипотеза
, то выдвинутая гипотеза 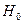 решительно отвергается, что свидетельствует о согласии линейной регрессивной связи с результатами наблюдений.
решительно отвергается, что свидетельствует о согласии линейной регрессивной связи с результатами наблюдений.
Так как линейная регрессия 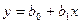 согласуется со статистическими данными, найдем (с надежностью g=0,95) доверительные интервалы для параметров
согласуется со статистическими данными, найдем (с надежностью g=0,95) доверительные интервалы для параметров 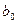 и
и  линейной регрессии. Для нахождения доверительных интервалов применим известные формулы:
линейной регрессии. Для нахождения доверительных интервалов применим известные формулы:
 ,
,
где 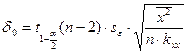 ,
, 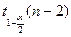 - квантиль распределения Стьюдента порядка
- квантиль распределения Стьюдента порядка 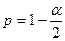 с k=n-2 степенями свободы,
с k=n-2 степенями свободы,  ;
;
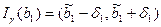 , где
, где 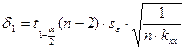 .
.
В данном случае 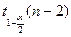 =
= 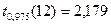 ,
,  ;
;

 ;
;
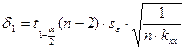 =
=  .
.
Применив приведенные выше формулы для доверительных интервалов, окончательно получим
 ,
,
 .
.
Задача 5.
Предположим, что в педагогическом эксперименте участвовали три группы студентов по 10 человек в каждой. В группах применили различные методы обучения: в первой – традиционный 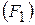 , во второй – основанный на компьютерных технологиях
, во второй – основанный на компьютерных технологиях  , в третьей – метод, широко использующий задания для самостоятельной работы
, в третьей – метод, широко использующий задания для самостоятельной работы 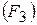 . Знания оценивались по десятибалльной системе.
. Знания оценивались по десятибалльной системе.
Требуется обработать полученные данные об экзаменах и сделать заключение о том, значимо ли влияние метода преподавания, приняв за уровень значимости  .
.
Результаты экзаменов заданы таблицей, 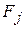 – уровень фактора
– уровень фактора  – оценка
– оценка  -го учащегося обучающегося по методике
-го учащегося обучающегося по методике 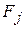 .
.
5.0.

| |||||||||||
Уровень фактора
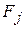
| 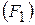
| ||||||||||
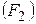
| |||||||||||

|
Поместим в таблице экзаменационные оценки (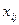 ), их отклонения от общей средней (
), их отклонения от общей средней ( ) и квадраты этих отклонений
) и квадраты этих отклонений  . Уровни фактора означают:
. Уровни фактора означают: 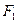 - традиционный метод,
- традиционный метод,  - применение компьютерной технологии,
- применение компьютерной технологии, 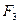 - увеличение доли самостоятельной работы.
- увеличение доли самостоятельной работы.
| Номер испытан.1 | Уровни фактора 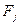 (различные методы преподавания) (различные методы преподавания)
| ||||||||
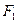
| 
| 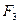
| |||||||
Оценки 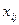
| 
| 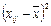
| Оценки 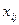
| 
| 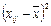
| Оценки 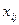
| 
| 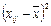
| |
| -1 | |||||||||
| -3 | -2 | ||||||||
| -1 | |||||||||
| -2 | -2 | ||||||||
| -3 | -1 | ||||||||
| -1 | -2 | ||||||||
| -2 | -1 | -1 | |||||||
| Груп. сред.2 | 5,9 | 8,2 | 6,9 | ||||||
| S |
1 Номер испытания (порядковый номер студента группы).
2 Групповая средняя (средний балл группы).
Общая средняя равна
 .
.
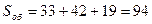 ;
; 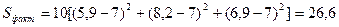 .
.
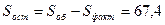 .
.
В нашем примере p=3 (p - количество факторов), q=10 (q - количество студентов), поэтому для степеней свободы получаются следующие значения: pq-1=29, p-1=2, p(q-1)=27.
Находим выборочные дисперсии: 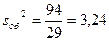 ;
; 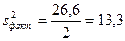 ;
;  .
.
Примем в качестве нулевой гипотезу о том, что выявленное различие групповых средних (средних баллов) случайно, т.е. при уровне значимости a=0,05 средние баллы совпадают.
Для проверки этой гипотезы следует воспользоваться F-критерием Фишера-Снедекора. Вычисляется  .
.
По таблицам находится критическая точка  . Здесь a - уровень значимости,
. Здесь a - уровень значимости, 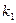 - число степеней свободы для дисперсии
- число степеней свободы для дисперсии  (в числитель формулы вписывается большая из дисперсий),
(в числитель формулы вписывается большая из дисперсий),  - число степеней свободы для меньшей дисперсии
- число степеней свободы для меньшей дисперсии 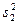 . В случае
. В случае 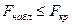 нулевая гипотеза принимается, в случае
нулевая гипотеза принимается, в случае 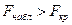 она отвергается.
она отвергается.
В примере 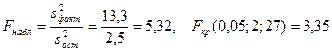 .
.
Таким образом, нулевая гипотеза отвергается, и следует считать, что средние баллы групп различаются "значимо". В частности, повышение качества знаний под воздействием уровня  фактора F нельзя считать случайным.
фактора F нельзя считать случайным.
Задача 6.
Группировка статистических данных.
По промышленным предприятиям города имеются следующие данные за отчетный год:
| № | Объем продукции, млн. руб. | Среднегодовая стоимость основных средств, млн. руб. | Среднесписочное число работников, чел. | Прибыль, млн. руб. |
| 478,0 | 19,1 | 112,2 | ||
| 207,3 | 9,6 | 30,2 | ||
| 194,4 | 8,9 | 30,4 | ||
| 462,3 | 18,3 | 97,3 | ||
| 207,1 | 10,1 | 33,2 | ||
| б | 196,5 | 10,0 | 13,4 | |
| 290,2 | 13,5 | 49,3 | ||
| 356,6 | 14,0 | 62,8 | ||
| 422,3 | 17,4 | 104,6 | ||
| 590,0 | 22,7 | 134,6 | ||
| 581,0 | 21,8 | 138,9 | ||
| 297,3 | 12,8 | 44,5 | ||
| 462,4 | 19,5 | 111,6 | ||
| 582,3 | 22,1 | 143,2 |
Требуется выполнить группировку предприятий по объему продукции, приняв следующие интервалы:
1)до 200 млн. руб.; 2) от 200 до 400 млн.руб.; 3) от 400 млн.руб. и более. По каждой группе и в целом по всем предприятиям определить:
- число предприятий;
- среднесписочное число работников;
- среднегодовую стоимость основных средств;
- объем продукции всего; средний объем продукции на одного работника; средний объем продукции на 1 млн. руб. стоимости основных средств;
- прибыль всего; среднюю прибыль на одного работника; среднюю прибыль на 1 млн. руб. стоимости основных средств.
Сделать вывод.
Для удобства вычислений заполняем сначала вспомогательную таблицу.
| Группы предприятий по объему продукции млн. руб. | Объем продукции, млн. руб. | Среднегодовая стоимость основных средств, млн. руб. | Среднесписочное число работников, чел. | Прибыль, млн. руб. |
| до 200 | 194,4; 196,5; | 8,9; 10,0; | 852; 900; | 30,4; 13,4; |
| от 200 до 400 | 207,3; 207,1; 290,2; 356,6; 297,3; | 9,6; 10,1; 13,5; 14,0;12,8; | 813;896; 1195; 1284; 1202; | 30,2; 33,2; 49,3; 62,8; 44,5; |
| более 400 | 478,0; 462,3; 422,3; 590,0; 581,0; 462,4; 582,3; | 19,1; 18,3; 17,4; 22,7; 21,8; 19,5; 22,1; | 1415; 1409; 1359; 1490; 1392; 1378; 1482; | 112,2; 97,3; 104,6; 134,6; 138,9; 111,6; 143,2; |
Результаты группировки приведены в следующей аналитической таблице.
| Группы предприятий по объему продукции млн. руб. | Число предприятий в группе | Среднесписочное число работников, чел. | Среднегодовая стоимость основных средств млн. руб. | Объем продукции | Прибыль | ||||
| Всего млн. руб. | В среднем на 1-го работника тыс. руб. | В среднем на 1 млн. руб. основных средств | Всего млн. руб. | В среднем на 1-го работника тыс. руб. | В среднем на 1 млн. руб. основных средств | ||||
| до 200 | 18,9 | 390,9 | 223,1 | 20,68 | 43,8 | 25,0 | 2,317 | ||
| от 200 до 400 | 60,0 | 1358,5 | 252,04 | 22,64 | 40,82 | 3,67 | |||
| более 400 | 140,9 | 3578,3 | 360,53 | 25,40 | 842,4 | 84,88 | 5,98 | ||
| Итого по всем группам | 219,8 | 5327,7 | 312,16 | 24,24 | 1106,2 | 64,82 | 5,03 |
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 419; Нарушение авторских прав?; Мы поможем в написании вашей работы!