
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Указания к выполнению контрольной работы 6 страница
|
|
|
|
Значения показателей объема продукции, прибыли, среднегодовой стоимости основных средств и среднесписочного числа работников по каждой группе и по всем предприятиям получаются суммированием соответствующих значений по каждому предприятию из вспомогательной таблицы.
Средние показатели объема продукции и прибыли на одного работника рассчитаны делением соответствующих суммарных показателей на число работников по группе (или по всем предприятиям). Аналогично рассчитаны средние показатели объема продукции и прибыли на один млн. руб. основных средств.
По результатам группировки, приведенной в аналитической таблице, можно сделать следующие выводы.
По объему продукции предприятия разделены на мелкие, средние и крупные. Доля мелких предприятий значительно ниже, чем доля средних и крупных.
Значение объема продукции в среднем на одного работника возрастает от мелких предприятий к крупным (I гр. - 223,1 тыс. руб., II гр. - 252,04 тыс. руб., III гр. - 360,53 тыс.руб.).
Еще более значительно растет прибыль на одного работника (I гр. - 25 тыс. руб., II гр. - 40,82 тыс. руб., III гр. - 84,88 тыс. руб.). На крупных предприятиях прибыль на одного работника в 3,4 раза выше, чем на мелких, и в два с лишним раза выше, чем на средних.
Аналогичная картина наблюдается и при сравнении объема продукции и прибыли в среднем на 1 млн. руб. основных средств. Так для крупных предприятий эта прибыль примерно в два с половиной (5,98:2,317ss2,58) раза больше, чем для мелких и в 1,6 раза больше, чем для средних.
Эти данные свидетельствуют о наибольшей эффективности предприятий третьей группы.
Задача 7.
Абсолютные, относительные и средние величины
По каждому из трех предприятий фирмы (г- порядковый номер предприятия), имеются соответствующие данные о фактическом объеме реализованной в 2000 г. продукции (у0 млн.руб.), о плановом задании по росту реализованной продукции на 2001 г. (8, %), а также о фактическом объеме реализованной в 2001 г. продукции (ух млн.руб.). Статистические данные приведены в таблице.
Требуется определить в целом по фирме:
1) размер планового задания по росту объема реализованной продукции в
2001 г;
2) процент выполнения плана по объему реализованной продукции в
2001г.;
3) показатель динамики реализованной продукции.
| i | y0i | δi% | y1i |
| 28,5 | 103,0 | ||
| 51,5 | 105,0 | 55,5 | |
| 62,5 | 102,5 | 63,0 |
При решении задачи используются следующие понятия: Относительный показатель динамики (ОПД) характеризует изменение явления во времени
ОПД= 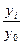 или в процентах ОПД=
или в процентах ОПД= 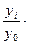 100%,
100%,
где у0 - базовый уровень исследуемого явления. В нашей задаче это объем реализованной продукции в 2000г; у i (i - 0,1,2,3,...) - уровень явления за одинаковые последовательные периоды времени (например, выпуск продукции по годам). ОПД иначе называются темпами роста. Они могут быть базовыми 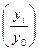 или цепными
или цепными 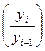 .
.
Относительный показатель плана ОПВП) - отношение величины показателя по плану (у пл) к его фактической величине в базисном (или предшествующем) периоде.
ОПП=  или ОПП=
или ОПП=  100%.
100%.
Относительный показатель выполнения плана (ОПВП) - отношение фактической (отчетной) величины показателя у 1к запланированной на тот же период времени его величине 
ОПВП= 
ОПД, ОПП и ОПВП связаны соотношением  или
или
опп·опвп=опд.
Решение задачи 7.
1. Найдем размер планового задания в целом по фирме по росту объема реализованной продукции в 2001 г., т.е. ОППф - относительный показатель плана фирмы.
Для этого найдем сначала плановое задание на 2001 г. по каждому предприятию 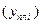 и в целом по фирме
и в целом по фирме 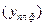
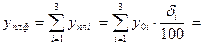 28,5·1,03+51,5·1,05+62,5·1,025=
28,5·1,03+51,5·1,05+62,5·1,025=
= 29,355 + 54,075 + 64,0625 = 147,4925 (млн.руб.).
Достигнутый в базисном периоде (2000г.) уровень в целом по фирме 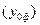
составляет 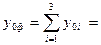 28,5 + 51,5 + 62,5 = 142,5 (млн.руб.)
28,5 + 51,5 + 62,5 = 142,5 (млн.руб.)
Теперь можно найти относительный показатель плана в целом по фирме на 2001г.
ОППф= 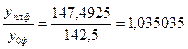
 или в процентах ≈103,5%.
или в процентах ≈103,5%.
2. Найдем процент выполнения плана по объему реализованной продукции в 2001 г. в целом по фирме (ОПВПф). Для этого найдем фактический уровень, достигнутый в 2001 г. 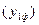
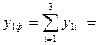 31 + 55,5 + 63,0 = 149,5 млн.руб., тогда
31 + 55,5 + 63,0 = 149,5 млн.руб., тогда
ОПВПф=  1,0136108 или 101,36%, т.е. план перевыполнен на 1,36%.
1,0136108 или 101,36%, т.е. план перевыполнен на 1,36%.
3. Найдем относительный показатель динамики реализованной продукции в целом по фирме (ОПДф)
ОПДф= 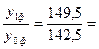 1,0491228 или ≈104,91%,
1,0491228 или ≈104,91%,
т.е. фактический рост составил ≈4,91%.
Проверка: ОПДф=ОППф·ОПВПф=1,035035·1,0136108=1,049123.
Задача 8.
Элементы дисперсионного анализа.
По каждой из трех основных рабочих профессий цеха (i -порядковый номер профессии: 1-токари; 2-фрезеровщики; 3-слесари) имеются соответствующие данные о числе рабочих профессии (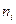 чел.), о средней заработной плате
чел.), о средней заработной плате
(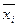 руб.), а также о внутригрупповой дисперсии заработной платы (
руб.), а также о внутригрупповой дисперсии заработной платы (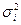 руб2). Статистические данные за месяц приведены в таблице.
руб2). Статистические данные за месяц приведены в таблице.
Требуется:
1)определить общую дисперсию заработной платы рабочих цеха;
2)оценить однородность совокупности рабочих цеха по уровню месячной заработной платы;
3)определить, на сколько процентов дисперсия в размере заработной платы обусловлена различиями в профессии рабочих и влиянием других причин.
| i | 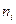
| 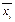
| 
|
Предварительные сведения.
Для характеристики величины вариации (колеблемости) признака статистической совокупности используются абсолютные и относительные показатели. В качестве абсолютных показателей чаще всего рассматривают дисперсию  и среднеквадратическое отклонение
и среднеквадратическое отклонение 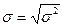 (СКО)
(СКО)
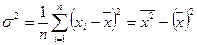 ,
,
где 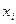 - наблюдённые значения признака (варианты), п - общее число вариант (объем выборки). Суммирование в этой формуле производится по всем вариантам;
- наблюдённые значения признака (варианты), п - общее число вариант (объем выборки). Суммирование в этой формуле производится по всем вариантам;  - среднее значение признака,
- среднее значение признака, 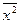 - среднее значение квадрата признака
- среднее значение квадрата признака
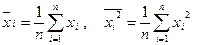 .
.
Изучая только общую дисперсию интересующего исследователя признака, нельзя оценить влияние отдельных факторов, как качественных, так и количественных, на величину признака. Это можно сделать при помощи метода группировки, когда варианты 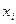 подразделяются на непересекающиеся группы по признаку-фактору. При этом, кроме общей средней
подразделяются на непересекающиеся группы по признаку-фактору. При этом, кроме общей средней  по всей выборке, рассматриваются средние по отдельным группам
по всей выборке, рассматриваются средние по отдельным группам 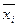 и следующие показатели дисперсии:
и следующие показатели дисперсии:
1.общая дисперсия 
2.межгрупповая дисперсия  ,
,
3.внутригрупповые дисперсии  ,
,
4.средняя внутригрупповая дисперсия  .
.
Кратко охарактеризуем эти дисперсии.
1. Общая дисперсия  учитывает влияние всех факторов, от которых зависит величина изучаемого признака X
учитывает влияние всех факторов, от которых зависит величина изучаемого признака X
 ,
,
где 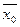 - общая средняя по всей выборке.
- общая средняя по всей выборке.
2. Межгрупповая дисперсия  (дисперсия групповых средних) отражает систематическую вариацию, т.е. те различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки. Эта дисперсия определяется по формуле:
(дисперсия групповых средних) отражает систематическую вариацию, т.е. те различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки. Эта дисперсия определяется по формуле:
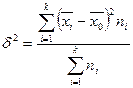
здесь 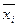 - внутригрупповые средние,
- внутригрупповые средние, 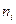 - число вариант в i -ой группе; к число групп, суммирование производится по различным группам.
- число вариант в i -ой группе; к число групп, суммирование производится по различным группам.
3. Внутригрупповая дисперсия
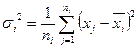
отражает рассеяние значений 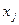 признака, относящихся к одному уровню группировочного фактора, поэтому она определяется не этим фактором, а другими причинами.
признака, относящихся к одному уровню группировочного фактора, поэтому она определяется не этим фактором, а другими причинами.
4. Средняя внутригрупповая дисперсия  , так же как и
, так же как и  , характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия, положенного в основу группировки. Эта дисперсия определяется по формуле
, характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия, положенного в основу группировки. Эта дисперсия определяется по формуле
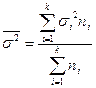 .
.
Можно доказать, что имеет место правило сложения дисперсий
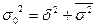
Отношение  показывает, какую долю общей дисперсии составляет
показывает, какую долю общей дисперсии составляет
дисперсия, возникающая под влиянием группировочного фактора, т.е. позволяет оценить влияние этого фактора на величину изучаемого признака X.
При сравнении колеблемости различных признаков в одной и той же совокупности или при сравнении колеблемости одного и того же признака в разных совокупностях используются относительные показатели вариации. Наиболее распространенным среди относительных показателей вариации является коэффициент вариации

Его применяют также и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).
Решение задачи 8.
1. Найдем среднюю из внутригрупповых дисперсий
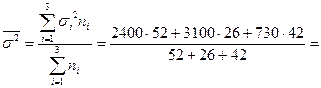 1967,17 (руб2).
1967,17 (руб2).
Определим среднюю зарплату по цеху для основных рабочих профессий (общую среднюю)
 2597,67(руб).
2597,67(руб).
Находим межгрупповую дисперсию
 =19438(руб2).
=19438(руб2).
Используя правило сложения дисперсий, найдем общую дисперсию заработной платы:
 = 19438 +1967 = 21405 (руб2).
= 19438 +1967 = 21405 (руб2).
2. Оценим однородность совокупности рабочих цеха по уровню месячной
заработной платы с помощью коэффициента вариации
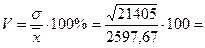 5,63%.
5,63%.
Так как V < 33 %, то совокупность считается однородной.
3. Общая дисперсия заработной платы рабочих цеха обусловлена различиями в профессии на
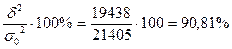 .
.
Эта же дисперсия обусловлена влиянием других причин на

Задача 9.
Элементы корреляционного анализа.
По 14-ти предприятиям городского хозяйства (i-порядковый номер предприятия) имеются соответствующие данные об объеме продукции (услуг) за месяц (у млн.руб.) и уровне механизации труда (х, %). Статистические данные
приведены в таблице.
Для выявления наличия корреляционной связи между объемом продукции
и уровнем механизации труда требуется:
1) измерить тесноту связи между признаками с помощью коэффициента
корреляции рангов Спирмена;
2) проверить его достоверность на уровне значимости α=0,05;

| ||||||||||||||

| ||||||||||||||
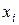
|
С помощью выборочного коэффициента ранговой корреляции Спирмена 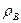 оценивается теснота связи между двумя качественными переменными X и Y. Этот коэффициент применяется и в случае количественных переменных, если заранее не гарантируется нормальность распределения двумерной случайной величины (X,Y).
оценивается теснота связи между двумя качественными переменными X и Y. Этот коэффициент применяется и в случае количественных переменных, если заранее не гарантируется нормальность распределения двумерной случайной величины (X,Y).
Выборочный коэффициент 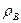 служит точечной оценкой генерального коэффициента ранговой корреляции
служит точечной оценкой генерального коэффициента ранговой корреляции  . Коэффициенты
. Коэффициенты 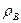 и
и  изменяются от минус единицы до плюс единицы. Чем ближе
изменяются от минус единицы до плюс единицы. Чем ближе  к 1, тем теснее связь между переменными X и Y.
к 1, тем теснее связь между переменными X и Y.
1. Для того чтобы вычислить коэффициент ранговой корреляции  , нужно сначала провести ранжировку объектов и получить две согласованные последовательности рангов.
, нужно сначала провести ранжировку объектов и получить две согласованные последовательности рангов.
Расположим наблюдаемые пары в порядке невозрастания качества по показателю X:

| ||||||||||||||

|
Затем пронумеруем объекты (числа) в каждой из строк в порядке неубывания. Рангом объекта называется его номер в ранжировке. Получим следующую таблицу:
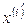
| ||||||||||||||

| 9 | 8 | 10 | 11 |
В первой ранжировке обведены группы объектов, имеющих одинаковое качество по переменной X; во второй ранжировке единообразно отмечены объекты, имеющие одинаковое качество по переменной Y.
Далее объектам одинакового качества присваиваем средние ранги (средние арифметические порядковых номеров этих объектов). В результате получим две согласованные последовательности рангов:

| 1,5 | 1,5 | 3,5 | 3,5 | 7,5 | 7,5 | 13,5 | 14,5 | ||||||
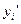
| 7,5 | 7,5 | ||||||||||||
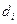
| -8,5 | -6 | -4 | -6,5 | -5 | -8 | 1,5 | -5,5 | 1,5 | 13,5 |
В последней строке записаны разности рангов 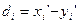 .
.
Найдем сумму квадратов разностей рангов:  =670,5 и по известной формуле вычислим выборочный коэффициент ранговой корреляции Спирмена:
=670,5 и по известной формуле вычислим выборочный коэффициент ранговой корреляции Спирмена:
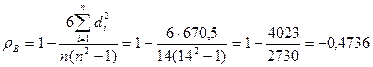
2) Для проверки статистической значимости выборочного коэффициента ранговой корреляции Спирмена на заданном уровне значимости αвыдвигается гипотеза Но об отсутствии ранговой корреляционной связи:
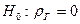 .
.
Для проверки выдвинутой гипотезы используется статистика Стьюдента
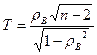 ,
,
где п - число пар (xi, y i)в выборке.
При условии справедливости гипотезы H0 случайная величина Т имеет известное t -распределение Стьюдента с к=п-2 степенями свободы.
Зная 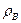 , вычисляем наблюдаемое значение статистики Стьюдента:
, вычисляем наблюдаемое значение статистики Стьюдента:
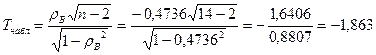
и число степеней свободы к = п - 2 = 12.
По таблице критических точек распределения Стьюдента для двусторонней критической области находим критическую точку статистики Стьюдента (см. например [4]),
 .
.
Критерий проверки:
1.Если  , то гипотеза H0 сохраняется (ранговая корреляционная связь практически отсутствует);
, то гипотеза H0 сохраняется (ранговая корреляционная связь практически отсутствует);
2.Если 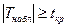 , то гипотеза Н 0 отвергается (существует значимая корреляционная связь между переменными X и Y).
, то гипотеза Н 0 отвергается (существует значимая корреляционная связь между переменными X и Y).
В нашем случае \Тнабл\ = 1,863 < 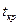 =2,18, поэтому в соответствие с критерием проверки заключаем, что
=2,18, поэтому в соответствие с критерием проверки заключаем, что  незначимо отличается от нуля, т.е. ранговая корреляционная связь практически отсутствует.
незначимо отличается от нуля, т.е. ранговая корреляционная связь практически отсутствует.
Задача 10.
Прогнозирование на основе сглаженного временного ряда
Динамика удельного расхода условного топлива на производство тепло-энергии (yt, кг/Гкал) на ТЭЦ по годам представлена в таблице. Требуется:
1)произвести сглаживание ряда методом трехлетней скользящей средней;
2)выровнять ряд по прямой - т.е. оценить параметры b o ,b 1линейного
тренда  = b0 + b 1 t методом наименьших квадратов;
= b0 + b 1 t методом наименьших квадратов;
3)начертить графики первичного и сглаженных рядов;
4)на уровне значимости α = 0,05 проверить согласованность линейной
трендовой модели с результатами наблюдений;
5)методом экстраполяции найти точечные и интервальные (с доверитель
ной вероятностью γ = 0,95) оценки прогноза экономического показателя yt на
2002 и 2003г.г.

| |||||||||
| yt | 169,2 | 168,1 | 168,6 | 168,4 | 167,9 | 167,6 | 167,8 | 166,9 | 167,1 |
(n=9)
Временным рядом называется последовательность значений (уровней) некоторого экономического показателя yt, расположенных в порядке возрастания времени. Уровни ряда должны отражать значения экономического показателя за одинаковые или через одинаковые промежутки времени.
Одной из важнейших задач исследования временного ряда является задача выявления основной тенденции развития (тренда) изучаемого процесса.
Решение этой задачи необходимо для прогнозирования. При этом исходят из того, что тенденция развития, установленная в прошлом, может быть распространена (экстраполирована) на будущий период.
Наиболее простыми и часто применяемыми способами выявления основной тенденции развития являются сглаживание временного ряда методом скользящей средней или выравнивание по прямой методом наименьших квадратов.
1) Метод скользящей средней основан на переходе от начальных значений членов ряда к их средним значениям на интервале времени, длина которого определена заранее. При этом сам выбранный интервал времени "скользит" вдоль ряда, получаемый таким образом ряд скользящих средних ведет себя более гладко, чем исходный ряд.
Для нашего примера скользящие средние находим по формуле
 .
.
Например, при t = 2
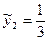 (169,2 +168,1 +168,9)
(169,2 +168,1 +168,9)  168,7,
168,7,
при t = 3 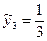 (168,1 +168,9 +168,4)
(168,1 +168,9 +168,4)  168,5.
168,5.
По результатам получим сглаженный ряд:

| |||||||||
| yt | – | 168,6 | 168,4 | 168,3 | 168,0 | 167,8 | 167,8 | 167,3 | – |
2) По статистическим данным найдем оценки  и
и 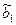 параметров линейного тренда
параметров линейного тренда 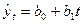 методом наименьших квадратов. Для этого применим известные формулы [1]:
методом наименьших квадратов. Для этого применим известные формулы [1]:
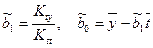 ,
,
где 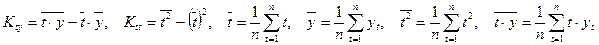 .
.
Здесь и в дальнейшем t - номер уровня ряда: 1993 г. соответствует номер 1,... 2001 году - номер 9.
Вычисление средних значений 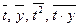 организуем в форме расчетной таблицы.
организуем в форме расчетной таблицы.

| yt | 
| 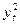
| 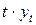
| |
| 169,2 | 28628,64 | 169,2 | |||
| 168,1 | 28257,61 | 336,2 | |||
| 168,6 | 28425,96 | 505,8 | |||
| 168,4 | 28358,56 | 673,6 | |||
| 167,9 | 28190,41 | 839,5 | |||
| 167,6 | 28089,76 | 1005,6 | |||
| 167,8 | 28156,84 | 1174,6 | |||
| 166,9 | 27855,61 | 1335,2 | |||
| 167,1 | 27922,41 | 1503,9 | |||
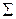
| 1511,6 | 253885,8 | 7543,6 | ||
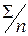
| 167,955 | 31,67 | 28209,53 | 838,18 | |
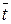
| 
| 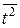
| 
| 
|
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 934; Нарушение авторских прав?; Мы поможем в написании вашей работы!