Указания к выполнению контрольной работы 7 страница

.

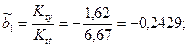
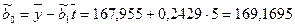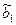Таким образом, искомые оценки параметров линейного аренда равны: = 169,1695, = -0,2429. Уравнение линейного тренда имеет вид:

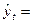169,1695 - 0,2429· t.

3)

(2)

На рисунке цифрой (1) отмечен первичный ряд, цифрой (2) - скользящая трехлетняя средняя, цифрой (3) помечен ряд, выровненный по прямой.

	(1)

(1)

4) Проверка согласованности линейной трендовой модели с результатами наблюдений выполняется как решение задачи проверки статистической гипотезы об отсутствии линейной статистической связи переменных 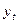и t на заданном уровне значимости α = 0,05. Для проверки гипотезы используется коэффициент детерминации и применяется статистика Фишера с 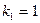и к ₂ =п - 2степенями свободы.

В рассматриваемом случае 28209,53 - (167,955)² = 0,648, , .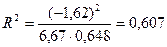

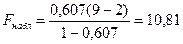Критическое значение статистики Фишера равно

.

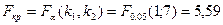Так как 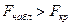, то выдвинутая гипотеза H_о отвергается, что свидетельствует о согласии линейной трендовой модели с результатами наблюдений.

5) По полученному уравнению линейного тренда =169,1695- 0,2429 t найдем точечные (индивидуальные) прогнозы показателя 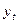на 2002 и 2003 г.г.

Для 2002г. t = 10

166,7405.

Для 2003г. t = 11

166,4976.

Дать интервальную оценку тренда - значит указать границы интервала, в который попадет возможное значение переменной 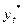с заданной доверитель­ной вероятностью γ(в нашем примере γ= 0,95).

Этот интервал определяется по известным формулам [3]

,

где δ- точность прогноза , здесь к=п- 2- число степеней свободы, α = 1-γ, ищется по таблице критических точек распределения Стьюдента для двусторонней критической области (см., например [4]); в нашем случае α=1 - 0,95 = 0,05; к = 9-2 =7; 2,36. (Можно воспользоваться так же таблицами 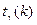[3]). 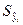- исправленное среднеквадратическое отклонение (С.К.О.) индивидуальных значений зависимой переменной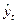

_.

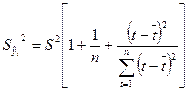Из этой формулы видно, чем больше , тем меньше точность прогноза. S - исправленное С.К.О. ошибок линейной регрессии

.

Вычисление доверительных интервалов прогнозов организуем в виде таблицы

t	yt
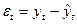
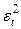
	169,2	168,9266	0,2734	0,07475
	168,1	168,6837	-0,5837	0,34071
	168,6	168,4408	0,1592	0,02534
	168,4	168,1979	0,2021	0,04084
	167,9	167,9550	-0,055	0,00303
	167,6	167,7121	-0,1121	0,01257
	167,8	167,4692	0,3308	0,10943
	166,9	167,2263	-0,3263	0,10647
	167,1	166,9834	0,1166	0,01360
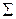
	–	–	–	0,72674

.

.

Дальнейшие вычисления проводим отдельно для t =10 (2002 г.) и t =11 (2003 г.)

Для t = 10

.

,

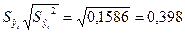
166,74-0,94< <166,74+0,94.

Итак, с вероятностью γ = 0,95, удельный расход условного топлива в 2002 г. будет принадлежать интервалу (кг/Гкал)

165,8 < < 167,68.

Аналогично для 2003 г. t = 11, получим

. , ,

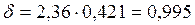166,498-0,995< <166,498+0,995. 165,50< <167,49, γ=0,95.

Приложение 1

Таблица значений функции Лапласа

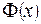
0,00	0,0000	0,32	0,1255	0,64	0,2389	0,96	0,3315
0,01	0,0040	0,33	0,1293	0,65	0,2422	0,97	0,3340
0,02	0,0080	0,34	0,1331	0,66	0,2454	0,98	0,3365
0,03	0,0120	0,35	0,1368	0,67	0,2486	0,99	0,3389
0,04	0,0160	0,36	0,1406	0,68	0,2517	1,00	0,3413
0,05	0,0199	0,37	0,1443	0,69	0,2549	1,01	0,3438
0,06	0,0239	0,38	0,1480	0,70	0,2580	1,02	0,3461
0,07	0,0279	0,39	0,1517	0,71	0,2611	1,03	0,3485
0,08	0,0319	0,40	0,1554	0,72	0,2642	1,04	0,3508
0,09	0,0359	0,41	0,1591	0,73	0,2673	1,05	0,3531
0,10	0,0398	0,42	0,1628	0,74	0,2703	1,06	0,3554
0,11	0,0438	0,43	0,1664	0,75	0,2734	1,07	0,3577
0,12	0,0478	0,44	0,1700	0,76	0,2764	1,08	0,3599
0,13	0,0517	0,45	0,1736	0,77	0,2794	1,09	0,3621
0,14	0,0557	0,46	0,1772	0,78	0,2823	1,10	0,3643
0,15	0,0596	0,47	0,1808	0,79	0,2852	1,11	0,3665
0,16	0,0636	0,48	0,1844	0,80	0,2881	1,12	0,3686
0,17	0,0675	0,49	0,1879	0,81	0,2910	1,13	0,3708
0,18	0,0714	0,50	0,1915	0,82	0,2939	1,14	0,3729
0,19	0,0753	0,51	0,1950	0,83	0,2967	1,15	0,3749
0,20	0,0793	0,52	0,1985	0,84	0,2995	1,16	0,3770
0,21	0,0832	0,53	0,2019	0,85	0,3023	1,17	0,3790
0,22	0,0871	0,54	0,2054	0,86	0,3051	1,18	0,3810
0,23	0,0910	0,55	0,2088	0,87	0,3078	1,19	0,3830
0,24	0,0948	0,56	0,2123	0,88	0,3106	1,20	0,3849
0,25	0,0987	0,57	0,2157	0,89	0,3133	1,21	0,3869
0,26	0,1026	0,58	0,2190	0,90	0,3159	1,22	0,3883
0,27	0,1064	0,59	0,2224	0,91	0,3186	1,23	0,3907
0,28	0,1103	0,60	0,2257	0,92	0,3212	1,24	0,3925
0,29	0,1141	0,61	0,2291	0,93	0,3238	1,25	0,3944
0,30	0,1179	0,62	0,2324	0,94	0,3264
0,31	0,1217	0,63	0,2357	0,95	0,3289

Продолжение приложения 1

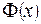
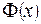
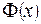
1,26	0,3962	1,59	0,4441	1,92	0,4726	2,50	0,4938
1,27	0,3980	1,60	0,4452	1,93	0,4732	2,52	0,4941
1,28	0,3997	1,61	0,4463	1,94	0,4738	2,54	0,4945
1,29	0,4015	1,62	0,4474	1,95	0,4744	2,56	0,4948
1,30	0,4032	1,63	0,4484	1,96	0,4750	2,58	0,4951
1,31	0,4049	1,64	0,4495	1,97	0,4756	2,60	0,4953
1,32	0,4066	1,65	0,4505	1,98	0,4761	2,62	0,4956
1,33	0,4082	1,66	0,4515	1,99	0,4767	2,64	0,4959
1,34	0,4099	1,67	0,4525	2,00	0,4772	2,66	0,4961
1,35	0,4115	1,68	0,4535	2,02	0,4783	2,68	0,4963
1,36	0,4131	1,69	0,4545	2,04	0,4793	2,70	0,4965
1,37	0,4147	1,70	0,4554	2,06	0,4803	2,72	0,4967
1,38	0,4162	1,71	0,4564	2,08	0,4812	2,74	0,4969
1,39	0,4177	1,72	0,4573	2,10	0,4821	2,76	0,4971
1,40	0,4192	1,73	0,4582	2,12	0,4830	2,78	0,4973
1,41	0,4207	1,74	0,4591	2,14	0,4838	2,80	0,4974
1,42	0,4222	1,75	0,4599	2,16	0,4846	2,82	0,4976
1,43	0,4236	1,76	0,4608	2,18	0,4854	2,84	0,4977
1,44	0,4251	1,77	0,4616	2,20	0,4861	2,86	0,4979
1,45	0,4265	1,78	0,4625	2,22	0,4868	2,88	0,4980
1,46	0,4279	1,79	0,4633	2,24	0,4875	2,90	0,4981
1,47	0,4292	1,80	0,4641	2,26	0,4881	2,92	0,4982
1,48	0,4306	1,81	0,4649	2,28	0,4887	2,94	0,4984
1,49	0,4319	1,82	0,4656	2,30	0,4893	2,96	0,4985
1,50	0,4332	1,83	0,4664	2,32	0,4898	2,98	0,4986
1,51	0,4345	1,84	0,4671	2,34	0,4904	3,00	0,49865
1,52	0,4357	1,85	0,4678	2,36	0,4909	3,20	0,49931
1,53	0,4370	1,86	0,4686	2,38	0,4913	3,40	0,49966
1,54	0,4382	1,87	0,4693	2,40	0,4918	3,60	0,49841
1,55	0,4394	1,88	0,4699	2,42	0,4922	3,80	0,499928
1,56	0,4406	1,89	0,4706	2,44	0,4927	4,00	0,499968
1,57	0,4418	1,90	0,4713	2,46	0,4931	4,50	0,499997
1,58	0,4429	1,91	0,4719	2,48	0,4934	5,00	0,499997

Приложение 2

Таблица значений функции

0,0	0,399
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0	0,242
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0	0,054
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0	0,004
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9

Приложение 3

Критические точки распределения

Число степеней свободы	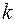Уровень значимости
0,01	0,025	0,05	0,95	0,975	0,99
	6,6	5,0	3,8	0,0039	0,00098	0,00016
	9,2	7,4	6,0	0,103	0,051	0,020
	11,3	9,4	7,8	0,352	0,216	0,115
	13,3	11,1	9,5	0,711	0,484	0,297
	15,1	12,8	11,1	1,15	0,831	0,554
	16,8	14,4	12,6	1,64	1,24	0,872
	18,5	16,0	14,1	2,17	1,69	1,24
	20,1	17,5	15,5	2,73	2,18	1,65
	21,7	19,0	16,9	3,33	2,70	2,09
	23,2	20,5	18,3	3,94	3,25	2,56
	24,7	21,9	19,7	4,57	3,82	3,05
	26,2	23,3	21,0	5,23	4,40	3,57
	27,7	24,7	22,4	5,89	5,01	4,11
	29,1	26,1	23,7	6,57	5,63	4,66
	30,6	27,5	25,0	7,26	6,26	5,23
	32,0	28,8	26,3	7,96	6,91	5,81
	33,4	30,2	27,6	8,67	7,56	6,41
	34,8	31,5	28,9	9,39	8,23	7,01
	36,2	32,9	30,1	10,1	8,91	7,63
	37,6	34,2	31,4	10,9	9,59	8,26
	38,9	35,5	32,7	11,6	10,3	8,90
	40,3	36,8	33,9	12,3	11,0	9,54
	41,6	38,1	35,2	13,1	11,7	10,2
	43,0	39,4	36,4	13,8	12,4	10,9
	44,3	40,6	37,7	14,6	13,1	11,5
	45,6	41,9	38,9	15,4	13,8	12,2
	47,0	43,2	40,1	16,2	14,6	12,9
	48,3	44,5	41,3	16,9	15,3	13,6
	49,6	45,7	42,6	17,7	16,0	14,3
	50,9	47,0	43,8	18,5	16,8	15,0

Дата добавления: 2014-12-08