Поразрядные способы перевода

Пример 3.

Пример 2.

Пример 1.

Перевод целых чисел делением на основание.

Пример 3.

Пример 2.

Пример 1.

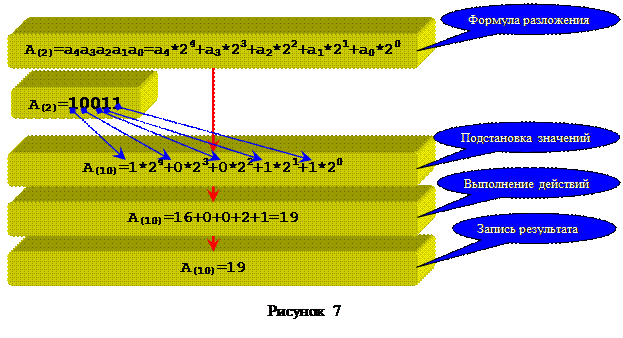
Дано A₍₂₎=10011. Найти A₍₁₀₎. Решение примера приведено на рисунке 7.

Дано A₍₈₎=257. Найти A₍₁₀₎.

Решение:

A₍₈₎= a₂a₁a₀=a₂*8²+a₁*8¹+a₀*8⁰

A₍₁₀₎= 2*64+5*8+7*1=128+40+7

A₍₁₀₎=175

Дано A₍₁₆₎=1EF6. Найти A₍₁₀₎.

Решение:

A₍₁₆₎= a₃a₂a₁a₀= a₃*16³+a₂*16²+a₁*16¹+a₀*16⁰

A₍₁₀₎= 1*4096+14*256+15*16+6*1=4096+3584+240+6

A₍₁₀₎=7926

Правило заключается в деление числа на основание с остатком, если остаток больше основания то он снова делиться на основание, до тех пор, пока остаток не станет меньше основания.

При этом способе перевода действия выполняются в исходной системе счисления, поэтому это способ удобен для перевода из десятичной системы счисления в остальные системы счисления.

Дано A₍₁₀₎=43. Найти A₍₂₎.

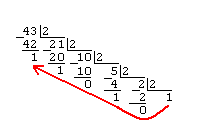
Ответ A₍₂₎=101011

Дано A₍₁₀₎=132. Найти A₍₈₎.

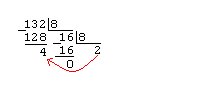
Ответ A₍₈₎=204

Дано A₍₁₀₎=213. Найти A₍₁₆₎.

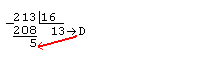
Ответ A₍₁₆₎=D5

Перевод чисел упрощается, если основание старой системы счисления p и новой системы счисления q связаны отношением:

p=q^k или q=p^k,

где:

p – основание исходной системы счисления;

q – основание результирующей системы счисления;

k – целое число.

Для систем счисления используемых в вычислительной технике значение k приведено в таблице 3.

Таблица 3.

Исходная система счисления	Результирующая система счисления	Значение k
Восьмеричная	Двоичная
Двоичная	Восьмеричная
Шестнадцатеричная	Двоичная
Двоичная	Шестнадцатеричная

При такой связи систем счисление перевод осуществляется с помощью таблиц 4 и 5.

Таблица 4.

Взаимосвязь восьмеричной и двоичной систем счисления.

Двоичная	Восьмеричная

Таблица 5.

Взаимосвязь шестнадцатеричной и двоичной систем счисления.

Шестнадцатеричная	Восьмеричная
	A
	B
	C
	D
	E
	F

Алгоритм поразрядного перевода из двоичной системы счисления в восьмеричную заключается в дроблении двоичного числа по три разряда с права на лево и замене соответствующими цифрами восьмеричной системы счисления из таблицы 4. Если в конце дробления остается меньше трех разрядов, то двоичное число дополняют с лева нулями. Алгоритм перевода представлен на рисунке 8.

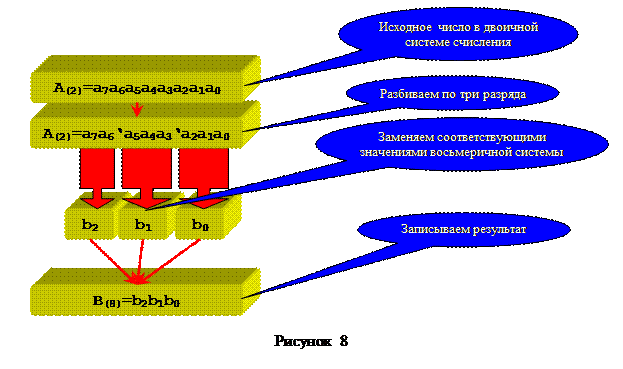
Обратный перевод из восьмеричной в двоичную систему счисления осуществляется по этому же алгоритму но в обратном порядке. Один разряд восьмеричной системы счисления заменяется тремя разрядами двоичной систем счисления.

Алгоритм перевода из двоичной в шестнадцатеричную систему счисления аналогичен алгоритму перевода в восьмеричную, за исключением того, что число дробиться не по три, а по четыре разряда и соответствия подбираются из таблицы 5.

Дата добавления: 2014-12-08