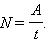Закон Кулона

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Тангенциа́льное ускоре́ние — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости. Равно произведению единичного вектора, направленного по скорости движения, на производную модуля скорости по времени. Таким образом, направлено в ту же сторону, что и вектор скорости при ускоренном движении (положительная производная) и в противоположную при замедленном (отрицательная производная).

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 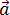_n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

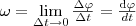
Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор d φ (рис. 2). Размерность угловой скорости dim ω = Т^-1, а ее единица — радиан в секунду (рад/с).

Линейная скорость точки (см. рис. 1)

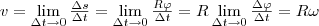
т.е

v = ωR

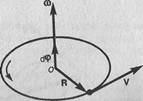
Рис.2

Угловым ускорением называется векторная величина, равная первой производной yгловой скорости по времени:

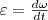
Тангенциальная составляющая ускорения a_τ=dv/dt, v = ωR и

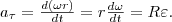
Нормальная составляющая ускорения

s = Rφ, v = Rω, а_τ = R, a_n = ω²R.

ДИНАМИКА, часть кинетики - раздела теоретической механики, в котором рассматриваются тела в условиях воздействия на них заданных сил.

СИЛА - физическое воздействие, приводящее или стремящееся привести к изменению состояния покоя или движения материального тела.

Материальная точка - идеализированная модель физического тела, размерами, структурой и формой которого можно пренебречь при решении поставленной задачи.

МАССА - мера инерционных и гравитационных свойств материальной точки.

Механическая система - совокупность материальных точек:

- движущихся согласно законам классической механики; и

- взаимодействующих друг с другом и с телами, не включенными в эту совокупность.

Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.

Второй закон Ньютона формулируется следующим образом: ускорение, приобретаемое материальной точкой (телом), прямо пропорционально действующей силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела):

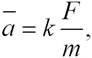(2.3)

где k - коэффициент пропорциональности, зависящий от выбора системы единиц. В международной системе (СИ) k =1, поэтому

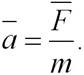(2.4)

Второй закон Ньютона обычно записывается в следующей форме:

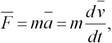
или

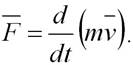(2.5)

Вектор mv=p называется импульсом или количеством движения. В отличие от ускорения и скорости, импульс является характеристикой движущегося тела, отражающей не только кинематическую меру движения (скорость), но и его важнейшее динамическое свойство – массу.

Таким образом, можно записать:

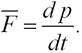(2.6)

Выражение (2.6) является более общей формулировкой второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе.
Это уравнение называется уравнением движения материальной точки.
Единица силы в системе СИ – ньютон (Н):
1 Н – это сила, которая телу массой в 1 кг сообщает ускорение 1 м/с² в направлении действия силы:

1 Н = 1 кг*1 м/с².

При действии на материальную точку нескольких сил справедлив принцип независимости действия сил: если на материальную точку действуют одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, определяемое вторым законом Ньютона так, как если бы других сил не было:

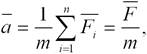
где сила 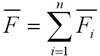называется равнодействующей сил или результирующей силой.
Таким образом, если на тело действует одновременно несколько сил, то, согласно принципу независимости действия сил, под силой F во втором законе Ньютона понимают результирующую силу.
Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго закона: в случае равенства нулю равнодействующей силы ускорение также равно нулю, т.е. тело находится в покое или движется равномерно.

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.

Центр масс — воображаемая точка С, положение которой характеризует распределение масс этой системы.

Закон движения центра масс — в инерциальных системах отсчёта центр масс системы движется как материальная точка, в которой находится масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.

; ;

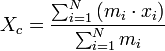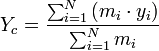Система центра масс — система отсчёта, относительно которой центр масс механической системы неподвижен.

Выведем уравнение движения тела переменной массы на примере движения ракеты. Если с момент времени t масса ракеты m, а ее скорость V,то по истечении времени dt ее масса уменьшится на dm и станет равной m-dm, а скорость станет равной V+dV. Изменение импульса системы за отрезок времени dt

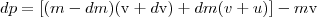
Тогда

Dp=mdV+Udm.

Если на систему действуют внешние силы, то dp=Fdt

Мы получили уравнение движения тела переменной массы

ma=F+Fр., которое впервые было выведено И.Б.Мещерским

V=U ln m0/m - это соотношение называется формулой Циолковского.

Она показывает, что:1) чем больше конечная масса, тем больше должна быть стартовая масса ракеты. 2) чем больше скорость истечения газов, тем больше может быть конечная масса при данной стартовой массе ракеты(U)

Получим уравнение движения тела переменной массы (например, движение ракеты сопровождается уменьшением ее массы за счет истечения газов, образующихся от сгорания топлива).
Пусть в момент времени t масса ракеты m, а ее скорость v; тогда по истечении времени dt ее масса уменьшится на dm и станет равной m–dm, а скорость увеличится до величины v+dv. Изменение импульса системы за время dt будет равно:

где u - скорость истечения газов относительно ракеты. Раскрывая скобки в этом выражении, получим:

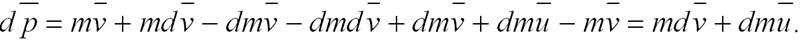
Если на систему действуют внешние силы, то 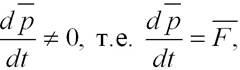или dp = Fdt. Тогда Fdt = mdv + udm, или

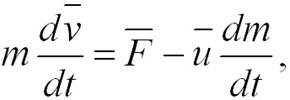(2.12)

где член 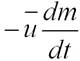называют реактивной силой F_p. Если вектор u противоположен v, то ракета ускоряется, а если совпадает с v, то тормозится.
Таким образом, уравнение движения тела переменной массы имеет следующий вид:

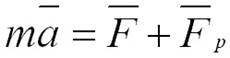(2.13)

Уравнение (2.13) называется уравнением И.В. Мещерского.
Применим уравнение (2.12) к движению ракеты, на которую не действуют никакие внешние силы. Тогда, полагая F = 0 и считая, что ракета движется прямолинейно (скорость истечения газов постоянна), получим:

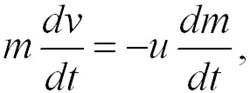
откуда

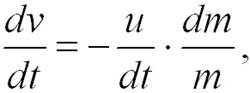
или

где С – постоянная интегрирования, определяемая из начальных условий. Если в начальный момент времени v =0, а стартовая масса ракеты составляет m₀, то C = u*ln m₀. Следовательно,

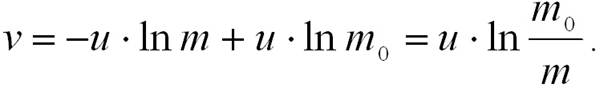(2.14)

Полученное соотношение называют формулой К.Э. Циолковского. Из выражения (2.14) следуют следующие практические выводы:
а) чем больше конечная масса ракеты m, тем больше должна быть стартовая масса m₀;
б) чем больше скорость истечения газов u, тем больше может быть конечная масса при данной стартовой массе ракеты.
Уравнения Мещерского и Циолковского справедливы для случаев, когда скорости v и u намного меньше скорости света c.

Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П₀ и П, одна из которых неподвижна, а другая жестко связана с телом.

φ=φ(t) – уравнение вращательного движения твердого тела.

Момент инерции- физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

I=m*R^2(полый тонкостенный цилиндр)

I=1/2m*R^2(сплошной цилиндр)

I=1/12m*l^2(прямой тонкий стержень,ось перпендикулярна стержню и проходит через середину)

I=1/3m*l^2(прям. Тонкий стержень, ось перепндик. И проходит через конец)

I=2/5m*R^2(шар. Ось проходит через центр)

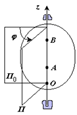
Рис. 1.3

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Теоре́маГю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математикаЯкоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела 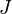относительно произвольной оси равен сумме момента инерции этого тела 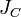относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела 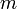на квадрат расстояния 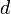между осями:

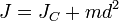
где

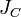— известный момент инерции относительно оси, проходящей через центр масс тела,

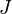— искомый момент инерции относительно параллельной оси,

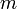— масса тела,

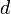— расстояние между указанными осями.

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.

Гироско́п — устройство, способное реагировать на изменение угловориентации связанного с ним тела относительно инерциальной системы координат, как правило, основанное на законе сохранения вращательного момента (момента импульса). Термин впервые введен Жаном (Бернаром Леоном) Фуко в его докладе в 1852 году Французской Академии Наук. Доклад был посвящён способам экспериментального обнаружения вращения Земли в инерциальном пространстве. Этим обусловлено и название «гироскоп»

Гироскопический эффект - это удержание (устойчивость) оси вращения объекта в пространстве. Этот эффект зависит от массы объекта, угловой скорости и от распределения моментов инерции. Если моменты инерции распределены немного неравномерно, то от этого будут возникать эффекты прецессии и нутации. Если моменты инерции распределены неравномерно, при этом ещё масса и угловая скорость объекта небольшие, тогда при эффекте прецессии ось объекта сначала описывает небольшую окружность, диаметр который всё время увеличивается. Затем ось объекта сама начинается вращаться в произвольных направлениях (кувыркаться).

Энергия - общая мера различных форм движения материи. Для количественной характеристики качественно различающихся форм движения и соответствующих им взаимодействий вводят различные виды энергии: механическую, внутреннюю, гравитационную, электромагнитную, ядерную и т.д…
Исходя из того, что любой материальный объект всегда находится в движении (находятся в движении определяющие его характеристики), что отражено в формулах 1 - 6 предыдущей главы установкой векторов, непротиворечивым шагом будет представление объекта в следующей математической форме:

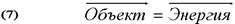
Т.е. согласуя проведенные ранее рассуждения с существующими определениями энергии, получаем полное и очевидное право поставить между понятиями объекта и энергии знак равенства. Для того, чтобы это право "ущемить", необходимо найти материальный объект, находящийся вне движения. По утверждениям главы 1 такого объекта в природе не существует. Кроме того, если взглянуть на определение энергии немного шире, то можно увидеть, что любая энергия представляет собой переход или возможность перехода объекта из одного состояния в другое путем взаимодействия с другим объектом. Описание и конкретное исследование любого вида энергии - это всего лишь оценка количественных и качественных изменений взаимодействующих объектов при их переходе (или при возможности перехода) в некоторое другое состояние. Согласуясь с результатами предыдущих рассуждений несложно заметить сходство поведения энергии с поведением того, что было определено, как объективная информация.

В физике механи́ческая эне́ргия описывает сумму потенциальной и кинетической энергии, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.

Работой A, совершаемой постоянной силой 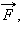называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус углаα между векторами силы 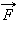и перемещения 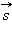(рис. 1.18.1):

A = Fs cos α.

Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).

Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.

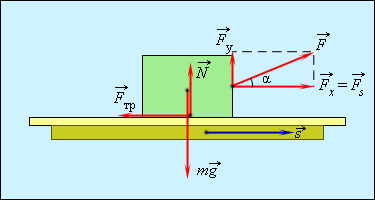
Рисунок 1.18.1. Работа силы :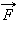

Если проекция силы 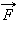на направление перемещения 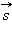не остается постоянной, работу следует вычислять для малых перемещений Δ s_i и суммировать результаты:

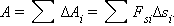
Это сумма в пределе (Δ s_i → 0) переходит в интеграл.

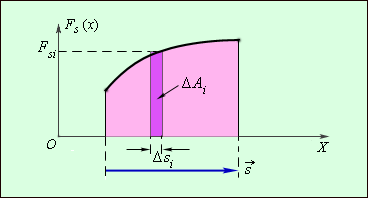
Графически работа определяется по площади криволинейной фигуры под графиком F_s (x) (рис. 1.18.2).

Рисунок 1.18.2. Графическое определение работы. Δ A_i = F_si Δ s_i

По площади треугольника можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:

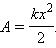
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы равна по модулю работе внешней силы 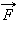и противоположна ей по знаку.

Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил.

Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.

Потенциальная энергия — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил.

Потенциальная энергия 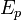в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

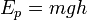
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

В физике консервати́вные си́лы — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.

Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется. Полная механическая энергия системы – сумма ее кинетической и потенциальной энергии.

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

E_k1 + E_p1 = E_k2 + E_p2.

Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.

Мо́щность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. Различают среднюю мощность за промежуток времени :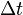

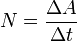
и мгновенную мощность в данный момент времени:

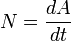
Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.

Основные кинематические характеристики вращательного движения тела — его угловая скорость () и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:

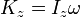
и кинетическая энергия

Преобразова́ния Галиле́я — в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой.. Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета и выполнение принципа относительности (Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе, преобразования Галилея приближенно верны с очень большой точностью.

Принцип относительности Галилея

Из формулы для ускорений следует, что если движущаяся система отсчета движется относительно первой без ускорения, то есть, то ускорение тела относительно обеих систем отсчета одинаково.

Поскольку в Ньютоновской динамике из кинематических величин именно ускорение играет роль, то, если довольно естественно предположить, что силы зависят лишь от относительного положения и скоростей физических тел, окажется, что все уравнения механики запишутся одинаково в любой инерциальной системе отсчета — иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-то конкретной из инерциальных систем отсчета. Также — поэтому — не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это утверждение известно как принцип относительности Галилея, в отличие от Принципа относительности Эйнштейна

Иным образом этот принцип формулируется (следуя Галилею) так: если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым.

Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.

Описываемые специальной теорией относительности отклонения в протекании физических процессов от предсказаний классической механики называют релятивистскими эффектами, а скорости, при которых такие эффекты становятся существенными, — релятивистскими скоростями.

Преобразованиями Лоренца в физике, в частности, в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой.

Пусть координатные оси двух инерциальных систем отсчёта S и S' параллельны друг другу, (t, x,y, z) — время и координаты некоторого события, наблюдаемого относительно системы S, а (t',x',y',z') — время и координаты того же события относительно системы S'. Если система S' движется равномерно и прямолинейно со скоростью v относительно S, то справедливы преобразования Лоренца:

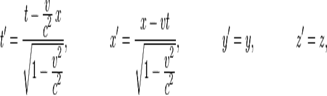
В СТО постулируется возможность определения единого времени в рамках данной инерциальной системы отсчёта. Для этого вводится процедура синхронизации двух часов, находящихся в различных точках ИСО. Пусть от первых часов, в момент времени 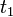ко вторым посылается сигнал (не обязательно световой) с постоянной скоростью 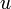. Сразу по достижении вторых часов (по их показаниям в момент времени 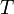) сигнал отправляется обратно с той же постоянной скоростью 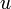и достигает первых часов в момент времени 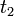. Часы считаются синхронизированными, если выполняется соотношение .

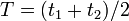Предполагается, что такая процедура в данной инерциальной системе отсчёта может быть проведена для любых неподвижных относительно друг друга часов, так что справедливо свойство транзитивности: если часы A синхронизованы с часами B, а часы B синхронизованы с часами C, то часы A и C также окажутся синхронизованными.

В отличие от классической механики единое время можно ввести только в рамках данной системы отсчёта. В СТО не предполагается, что время является общим для различных систем. В этом состоит основное отличие аксиоматики СТО от классической механики, в которой постулируется существование единого (абсолютного) времени для всех систем отсчёта.

Пространство в инерциальных системах отсчёта предполагается изотропным (нет выделенных направлений). Это приводит к тому, что 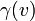является чётной функцией скорости: .

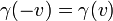Рассмотрим, например, измерение длины некоторого объекта (линейки), неподвижного в системе отсчёта S'. Если одновременно 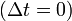в системе S измерить координаты «начала» и «конца» линейки, то её длина не должна зависеть от направления (знака) скорости 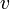, откуда следует, что функция 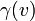является чётной.

Релятивистская динамика свободной частицы определяется полностью поведением ее вектора состояния при преобразованиях g квантово-механической группы Пуанкаре - Знание явного вида оператора U (g), действующего на вектор состояния частицы, равносильно решению уравнения движения для свободной частицы.

В релятивистской динамике теория, связанная со свободной частицей, не тривиальна, ибо она служит для того, чтобы связать физические понятия и математическую схему.

В релятивистской динамике, как и в ньютоновской, принимается, что импульс р материальной точки пропорционален ее массе т и совпадает по направлению со скоростью v этой точки.

Основное уравнение релятивистской динамики позволяет найти закон действующей на частицу силы F, если известна зависимость от времени релятивистского импульса p (t), а с другой стороны, найти уравнение движения частицы r (t), если известны действующая сила и начальные условия - скорость VQ и положение TO частицы в начальный момент времени.

С помощью релятивистской динамики можно, исходя из данного состояния в любой момент времени, построить новое состояние, соответствующее новому моменту времени. Однако в релятивистской динамике уравнением движения является уравнение, которое инвариантно относительно преобразований Лоренца по определению, а сила F не инвариантна.

К сожалению, релятивистская динамика вносит в это заключение свою поправку. Но эта масса неограниченно растет при приближении скорости движения к световой; соответственно увеличивается и продолжительность полуоборота. Следовательно, при постоянстве частоты генератора нарушается необходимое условие ускорения частицы - синхронизм между ее вращением и переменами полярности электродов.

Электри́ческий заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. Впервые электрический заряд был введён в законе Кулона в 1785 году.

Единица измерения заряда в СИ — кулон — электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1 с. Заряд в один кулон очень велик. Если бы два носителя заряда (q ₁ = q ₂ = 1 Кл) расположили в вакууме на расстоянии 1 м, то они взаимодействовали бы с силой 9·10⁹ H.

Электрический заряд дискретен, то есть заряд любого тела составляет целое кратное от элементарного электрического заряда

Электрический заряд замкнутой системы^[5] сохраняется во времени и квантуется — изменяется порциями, кратными элементарному электрическому заряду, то есть, другими словами, алгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему, не изменяется при любых процессах, происходящих в этой системе.

Закон сохранения заряда — один из основополагающих законов физики. Закон сохранения заряда был впервые экспериментально подтверждён в 1843 году великим английским ученым Майклом Фарадеем и считается на настоящее время одним из фундаментальных законов сохранения в физике (подобно законам сохранения импульса и энергии). Всё более чувствительные экспериментальные проверки закона сохранения заряда, продолжающиеся и поныне, пока не выявили отклонений от этого закона.

Дата добавления: 2014-12-16