Работа сил магнитного поля по перемещению проводника и контура с током

Вопрос

Вопрос

Вопрос

Магни́тный пото́к — поток 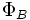вектора магнитной индукции 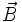через конечную поверхность 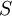определяется как интеграл по поверхности

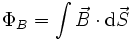
Силовые линии электрических и магнитных полей - линии, касательные к которым в каждой точке поля совпадают с направлением напряженности электрического или соответствующего магнитного поля; качественно характеризуют распределение электромагнитного поля в пространстве. Силовые линии - только наглядный способ изображения силовых полей.

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю: (теорема гаусса)

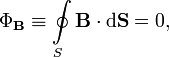
или в дифференциальной форме

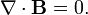
Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. Лаплас показал также, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда.

Допустим требуется найти модуль магнитной индукции в центре очень тонкой (все витки уложены вблизи одной окружности) катушки с числом витков 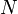, по которой течет ток 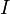. Найдём магнитную индукцию, создаваемую одним витком катушки. Из формулы

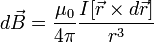
получим модуль магнитной индукции как

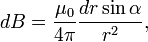
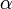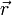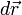где - как следствие, радиус катушки - константа, - угол между вектором и (элемента витка), ввиду взаимной перпендикулярности, всегда равен 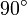. Проинтегрировав обе части получаем

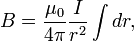
где 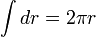- сумма длин всех элементов проводника витка или длина окружности, тогда

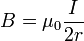
Так как в катушке содержится 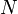витков, то суммарный модуль магнитной индукции равен

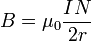
Формулировка теоремы о циркуляции
Пусть контур произвольной формы охватывает произвольное число токов. В этом случае теорема о циркуляции утверждает, что циркуляция вектора по некоторому (произвольному!) контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ, т.е.

.

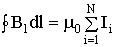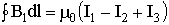
Применение теоремы о циркуляции приводит к соотношению:

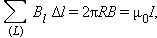
откуда следует формула для модуля магнитной индукции поля прямолинейного проводника с током, приведенная ранее.

Этот пример показывает, что теорема о циркуляции вектора магнитной индукции 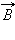может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля.

Имеется немало практически важных примеров расчета магнитных полей с помощью теоремы о циркуляции. Одним из таких примеров является задача вычисления поля тороидальной катушки

Предполагается, что катушка плотно, то есть виток к витку, намотана на немагнитный тороидальный сердечник. В такой катушке линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса r ₁ ≤ r < r ₂ изображена на рис. 1.17.3. Применим теорему о циркуляции к контуру L в виде окружности, совпадающей с изображенной на рис. 1.17.3 линией индукции магнитного поля. Из соображений симметрии ясно, что модуль вектора одинаков вдоль всей этой линии. По теореме о циркуляции можно записать:

B ∙ 2π r = μ₀ IN,

где N – полное число витков, а I – ток, текущий по виткам катушки. Следовательно,

Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, то есть r ₂ – r ₁ << r, то магнитное поле внутри катушки практически однородно. Величина n = N / 2π r представляет собой число витков на единицу длины катушки. В этом случае

B = μ ₀ I n.

36 вопрос:

Для удобства предположим, что контур имеет прямоугольную форму.

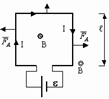
1) Пусть dl перпендикулярен B, т. е. любой элемент контура перпендикулярен силовым линиям. Cилы Ампера, действующие на каждый прямолинейный участок контура, указаны на рисунке.

Если контур с током расположен перпендикулярно силовым линиям, то действие поля выражается в сжимании и разжимании контура. Если же контур состоит из упругого проводника, то внешнего изменения положения в пространстве не будет.

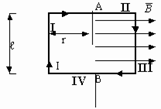
2) площадь контура с током параллельна силовым линиям. То есть нормаль плоскости контура перпендикулярна вектору магнитной индукции.

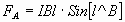
Тогда силы Ампера на каждом участке:

I. Sin=1, F_A≠0, сила направлена от нас.

II, IV. Sin=0, F_A=0, То есть на элемент контура с током лежащим вдоль силовых линий F_A не действует.

III Sin=1, F_A≠0, сила направлена к нам. Тогда если контур с током закрепить в точках A и B,то при таком расположении его в магнитном поле он будет вращаться, то есть на него действует момент силы.

Допустим, что провод с током может свободно перемещаться во внешнем магнитном поле под действием силы Ампера. Это можно осуществить с помощью скользящих контактов между концами провода и остальными участками замкнутой цепи (рис. 5.29). Внешнее поле будем пред­ полагать однородным и направленным перпендикулярно к плоскости рисунка.

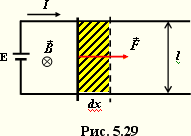
При указанных на рисунке направлениях тока и магнитного поля сила Ампера будет направлена вправо и равна

F = IBl,

где l – длина перемещающегося участка тока. На пути 444b15je dx эта сила совершает над проводни­

ком работу

dA = Fdx = IBldx.

Произведение ldx равно заштрихованной площади (рис. 5.29), а Bldx –потоку магнитной индукции dФ через эту площадку. Поэтому можно записать

dA = IdФ, (5.38)

где dФ – поток магнитной индукции, пересекаемый проводником при его движении. Полученный результат легко обобщить на случай неоднородного поля. Для этого нужно

разбить проводник на участки dl и сложить элементарные работы, совершаемые над каждым участком (в пределах каждой площадки dldx магнитную индукцию можно считать постоянной).

_{Если вектор 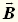образует с нормалью к поверхности, очерчиваемой проводником, угол a,}

отличный от нуля, направление силы составит с направлением перемещения также угол a и

dA = F cos a dx = IB_ndldx,

где B_n = B cos a – составляющая вектора магнитной индукции, по направлению к нормали к площадке dldx. Произведение B_ndldx есть dФ – магнитный поток, пересекаемый элементом про­ водника. Таким образом и в этом случае мы приходим к формуле (5.38)

Дата добавления: 2014-12-16