
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Занятие 1. Математический анализ
|
|
|
|
Математический анализ.
1. Функция. Область определения.
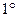 Понятие функции. Пусть Х и У – два множества вещественных чисел. Если каждому элементу х из множества Х по некоторому правилу ставится в соответствие единственное число
Понятие функции. Пусть Х и У – два множества вещественных чисел. Если каждому элементу х из множества Х по некоторому правилу ставится в соответствие единственное число 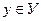 , то говорят, что на множестве Х задана функция, область значения которой расположена в У. Это можно записать так:
, то говорят, что на множестве Х задана функция, область значения которой расположена в У. Это можно записать так:
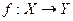 .
.
Множество Х- называют областью определения функции, а множество У, состоящее из всех чисел вида 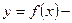 множеством значений функции.
множеством значений функции.
Если у является функцией от х, то пишут 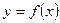 . Область определения обозначается через
. Область определения обозначается через 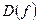 , а множество значений – через
, а множество значений – через 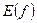 .
.
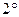 Основные элементарные функции. Основными элементарными функциями называют следующие функции:
Основные элементарные функции. Основными элементарными функциями называют следующие функции:
1) степенная функция  ,
, 
2) показательная функция 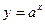 , где а- любое положительное число, отличное от единицы:
, где а- любое положительное число, отличное от единицы: 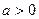 ,
, 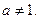
3) логарифмическая функция 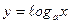 , где а- любое положительное число, отличное от единицы:
, где а- любое положительное число, отличное от единицы: 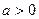 ,
, 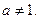
4) тригонометрические функции: 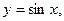
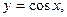
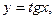
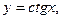
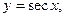
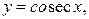
5) обратные тригонометрические функции: 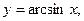
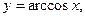
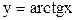
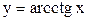 ,
,  ,
, 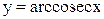 .
.
Элементарными называются функции, получающиеся из основных элементарных функций с помощью четырёх арифметических действий и применённых конечное число раз.
Пример неэлементарной функции:
|
|
|
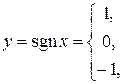
Графиком функции 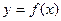 называется множество точек плоскости хОу с координатами
называется множество точек плоскости хОу с координатами 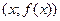 , где
, где 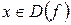 .
.
Функция 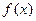 , область определения которой симметрична относительно нуля, называется чётной, если
, область определения которой симметрична относительно нуля, называется чётной, если 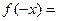
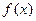 для
для 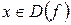 и нечётной, если
и нечётной, если 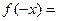
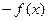 ,
, 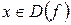 .
.
Произведение двух нечетных функций является четной функцией.
Функция 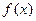 называется периодической, если существует положительное число Т такое, что при
называется периодической, если существует положительное число Т такое, что при 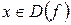 и
и 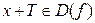 выполняется равенство
выполняется равенство 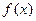 =
= 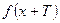 .
.
Пример 1. Найти область определения функции 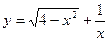 .
.
Решение. Данная функция определена, если 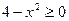 и
и 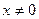 . Решаем эту систему:
. Решаем эту систему:
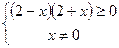
 |
Ясно, что искомое неравенство имеет место при 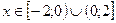 , значит полученное множество есть область определения данной функции.
, значит полученное множество есть область определения данной функции.
Пример 2. Установить чётность или нечётность функции 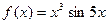 .
.
Решение. Для данной функции область определения симметрична относительно нуля: 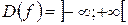 .
.
Заменяя х на –х, получим 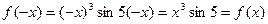 , т.е.
, т.е. 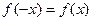 . Итак, данная функция чётная.
. Итак, данная функция чётная.
Пример 3. Найти основной период функции 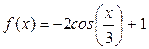 .
.
Решение. Так как основной период функции 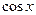 есть
есть 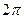 , то основной период функции
, то основной период функции 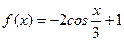 есть
есть  , т.е.
, т.е. 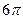 .
.
Контрольные вопросы.
1.Элементарные функции и их графики.
2.Понятие функции. Область определения.
Задания.
1) Найти область определения функции:
а) 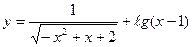 б)
б) 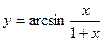
в) 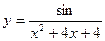 г)
г) 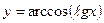 .
.
2) Какая из функций является чётной, какая нечётной:
а) 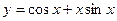 б)
б) 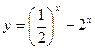
г) 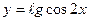 д)
д) 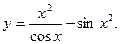
3) Найти периоды функций:
а) 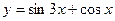 , б)
, б) 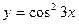 .
.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 426; Нарушение авторских прав?; Мы поможем в написании вашей работы!