
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Занятие 5
|
|
|
|
Производная функции.
Решение.
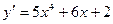 ;
;  ;
;
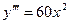 ;
; 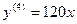 ;
;  ;
;
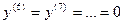 .
.
Пример 11. Дана функция 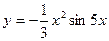
Найти:  .
.
Решение. 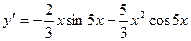 ,
,
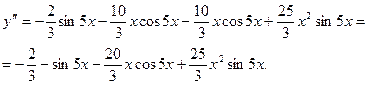
Контрольные вопросы.
2.Основные правила дифференцирования.
3.Производная обратной функции.
4.Формулы дифференцирования основных элементарных функций.
5.Понятия дифференциала функции.
6.Применение дифференциала к приближенным вычислениям.
7.Производные высших порядков.
Задания.
1. Пользуясь определением производной вычислить производные следующих функций:
1) 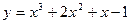 ;
;
2)  .
.
2. Найти производные и дифференциалы следующих функций
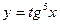 ;
;  ;
; 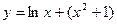 ;
; 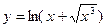 ;
;
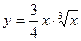 ;
;  ;
;  ;
;
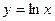 ;
; 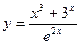 .
.
3.Найти производные функций:
1)  ;
;
2) 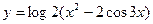 ;
;
3)  ;
;
4) 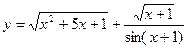 .
.
4.Найти 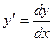 ,
,
1) если 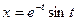 ,
,  ;
;
2) если  ,
, 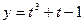 ;
;
3) если 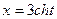 ,
,  .
.
5.Вычислить с помощью дифференциала приближенные значения
 ,
, 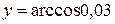 ,
, 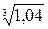 ,
, 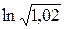 .
.
6.Найти производные
1)обратных тригонометрических функций
 ;
;  ;
;  ;
;  ;
;  .
.
2) 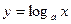 обратную к
обратную к 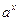 .
.
7. Найти 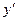 ,
,  ,
, 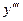 ,…,
,…,  для функций:
для функций:
1) 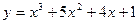 . 2)
. 2) 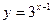 . 3)
. 3)  . 4)
. 4) 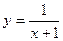 .
.
1. Теоремы Ролля, Лагранжа, Коши. Фрмула Тейлора.
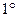 Теорема Ролля. Если функция
Теорема Ролля. Если функция 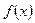 непрерывна на отрезке
непрерывна на отрезке 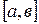 , дифференцируема в интервале
, дифференцируема в интервале  и
и  то в интервале
то в интервале  найдётся хотя бы одно значение
найдётся хотя бы одно значение  , при котором
, при котором 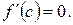
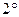 Теорема Лагранжа (о конечном приращении). Если функция
Теорема Лагранжа (о конечном приращении). Если функция 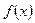 непрерывна на отрезке
непрерывна на отрезке 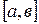 , дифференцируема в интервале
, дифференцируема в интервале 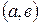 , то в этом интервале найдётся хотя бы одно значение
, то в этом интервале найдётся хотя бы одно значение 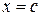 , при котором выполняется равенство
, при котором выполняется равенство  (геометрический смысл: касательная в точке
(геометрический смысл: касательная в точке  параллельна секущей АВ).
параллельна секущей АВ).
 Теорема Коши. Если функции
Теорема Коши. Если функции 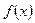 и
и  непрерывны на отрезке
непрерывны на отрезке  и дифференцируемы в интервале
и дифференцируемы в интервале  , причём
, причём 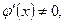 то в этом интервале найдётся хотя бы одно значение
то в этом интервале найдётся хотя бы одно значение 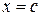 , при котором
, при котором  где
где 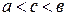 .
.
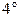 Формула Тейлора. Если функция
Формула Тейлора. Если функция 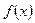 имеет в точке
имеет в точке  все производные до порядка
все производные до порядка  включительно, то
включительно, то
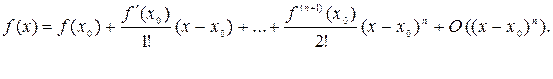
Это соотношение называется формулой Тейлора с остаточным членом в форме Пеано.
При  = 0 получаем частный случай формулы Тейлора- формулу Маклорена
= 0 получаем частный случай формулы Тейлора- формулу Маклорена 
Приведем разложение некоторых функций по формуле Маклорена:
 ,
,
 ,
,

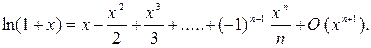
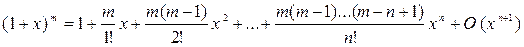
Пример 1. Выполняется ли теорема Ролля для функции 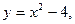
если а=-3; в=3. Найти значение  .
.
Решение. Так как функция 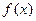 непрерывна и дифференцируема при всех значениях х и её значения на концах отрезка
непрерывна и дифференцируема при всех значениях х и её значения на концах отрезка  равны
равны  Следовательно, условия теоремы Ролля на этом отрезке выполняются. Значение
Следовательно, условия теоремы Ролля на этом отрезке выполняются. Значение  определяем из уравнения
определяем из уравнения 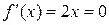 , т.е.
, т.е.  .
.
Пример 2. На дуге АВ кривой  найти точку М, в которой касательная параллельна хорде АВ, если А(1,3) и В(3,3).
найти точку М, в которой касательная параллельна хорде АВ, если А(1,3) и В(3,3).
Решение. Функция  непрерывна и дифференцируема при всех значениях х. По теореме Лагранжа между двумя значениями а=1 и в=3 существует значение х=
непрерывна и дифференцируема при всех значениях х. По теореме Лагранжа между двумя значениями а=1 и в=3 существует значение х=  , удовлетворяющее равенству:
, удовлетворяющее равенству:
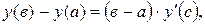
где 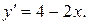
Подставив соответствующие значения, получим

Отсюда 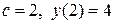 . Таким образом, точка М имеет координаты М(2;4).
. Таким образом, точка М имеет координаты М(2;4).
Пример 3. Проверить теорему Коши для функции 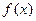 =х3 и
=х3 и 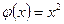 и найти с.
и найти с.
Решение. Из формулы Коши имеем
 , т.е.
, т.е.  .
.
Отсюда, получим  .
.
Пример 4. Разложить функцию 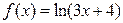 по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки 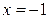 .
.
Решение. Представим, данную функцию в виде
 .
.
Далее воспользуемся формулой  .
.
Будем иметь
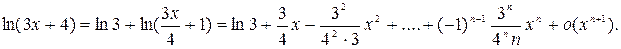
Пример 5. Вычислить предел, используя разложение по формуле Тейлора
 .
.
Решение. Так как
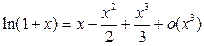 и
и  то получим
то получим

Контрольные вопросы.
1. Теоремы Ролля, Лагранжа, Коши.
2.Формула Тейлора. Формула Маклорена.
3.Разложение элементарных функций в ряд Маклорена.
Задания.
1. Применима ли теорема Ролля к функции  на отрезке
на отрезке  . Пояснить графически.
. Пояснить графически.
2. Проверить теорему Лагранжа и найти с для функций: а)  на отрезке
на отрезке 
б) 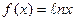 на отрезке
на отрезке 
3.Проверить теорему Коши и найти с для функций: а) 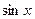 и
и 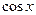 на отрезке
на отрезке  ,
,
б) х2 и  на отрезке
на отрезке 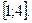 .
.
4. Разложить функцию 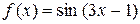 по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки 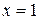 .
.
5. Найти пределы, используя разложение по формуле Тейлора
а)  ,
,
б)  .
.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 528; Нарушение авторских прав?; Мы поможем в написании вашей работы!