Малые колебание механической с-мы с учётом сил сопротивления

Они описываются ур-ием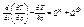

где 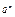- часть обобщённой силы, зависящей от потенциальной силы.

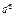- часть обобщённой силы, зависящей от действия сил сопротивления.

Линейные силы сопротивления 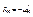, т.е. пропорциональны скорости, где μ – коэффициент, характеризующий св-ва вязкой среды, либо соприкасающихся трущихся поверхностей. По определению обобщённой силы запишем 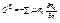. Используя тождество Лагранжа и меняя порядок суммирования, получаем: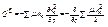

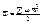-ф-ция Релея, характеризует скорость убывания полной энергии с-мы в зависимости от сил сопротивления. .

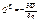Возьмём функцию Релея в виде: .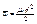

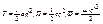
Произведём все операции дифференцирования и подстановки в ур-ие Лагранжа:

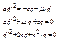
где 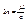, n – обобщённый коэффициент сопротивления системы.

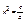-циклическая частота.

Получаем ДУ 2-го порядка без правой части, решение которой зависит от вида корней характеристического уравнения, характеризует колебания движения системы с учётом сил сопротивления.

Составим такое уравнение

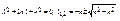
Возможны 3 случая:

1) n<k

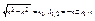
Если корни такие (мнимые), то решение ищем в виде:

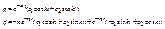
При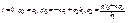

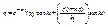- ур-ие затухающих колебаний.

В амплитудной форме: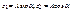

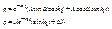
α – начальная фаза колебаний

А – условная амплитуда колебаний

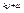-фаза.

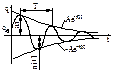
Важной характеристикой затухающих колебаний является отношение 2-х последовательных максимумов – декремент затухания 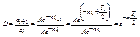-логарифмический декремент затухания – величина обратная числу колебаний, за которое время амплитуда уменьшается в е раз.

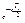-знаменатель геометрической прогрессии.

2) n>k

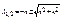. Оба корня действительные и отрицательные.

Решение ищем в виде 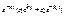. Для определения c1 и c2 дифференцируем ур-ие и при t=0 определяем. Движение носит апериодический характер.

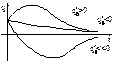
3) n=k – случай критического сопротивления 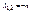. Ур-ие получаем в виде 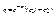. c1 и c2 определяются дифференцированием. Движение носит апериодический характер.

Дата добавления: 2014-12-16