Обобщенные силы

Элементарная работа внешних сил, приложенных к точкам системы, на возможных перемещениях точек этой системы определяется следующим выражением

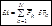(7.3)

Пусть голономная система имеет K степеней свободы и, следовательно, ее положение можно определять обобщенными координатами: .

Тогда, имея в виду, что и (7.2) получаем, что .

Тогда (7.4)

Выражение (7.3) с учетом (7.4) можно записать

(7.5)

где скалярная величина (7.5,а)

называется обобщенной силой, отнесенной к обобщенной координате .

Обобщенную силу (7.5,а) можно переписать

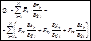(7.6)

Приступим к выводу дифференциальных уравнений движения голономной системы в обобщенных координатах . Будем исходить из общего уравнения динамики (6.3)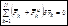

или (7.7)

Первое слагаемое в выражении (7.6) запишем через обобщенную силу, согласно (7.5):

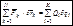(7.8)

Запишем второе слагаемое (7.5) через обобщенные координаты. Имеем

(7.9)

Распишем .

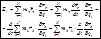(7.10)

в чем легко убедиться непосредственным дифференцированием.

Докажем, что выполняется следующее соотношение:

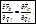(7.11)

Действительно, 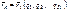, тогда

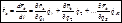(7.12)

Так как множители 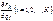зависят только от обобщенных координат (и не зависят от обобщенных скоростей), то, дифференцируя равенство (7.11) по обобщенным скоростям, получаем, что

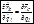следовательно, равенство (7.11) доказано.

Далее, имеем (7.13)

Возвращаясь к формуле (7.9) и подставляя в нее (7.11) и (7.13), получаем

Здесь 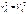– скорость k -ой точки; – кинетическая энергии механической системы.

Итак, получили, что

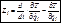(7.14)

Тогда общее уравнение динамики (7.7) в обобщенных координатах, с учетом (7.8) и (7.9) имеет вид:

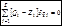(7.15)

Так как – независимые координаты, то равенство (7.15) может иметь место только тогда, когда все коэффициенты при 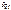в этом уравнении равны нулю. Поэтому общее уравнение динамики (7.15) эквивалентно системе уравнений 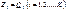, которые, согласно (7.8) и (7.14), могут быть записаны в следующем виде:

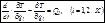(7.16)

Уравнения (7.16) носят название уравнений Лагранжа второго рода.

Величина 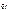– называется обобщенной скоростью; 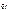– обобщенным ускорением.

Уравнения Лагранжа второго рода (7.16) образуют систему из K обыкновенных дифференциальных уравнений второго порядка с K неизвестными. Напомним, что K – число степеней свободы рассматриваемой механической системы.

Итак, число уравнений Лагранжа второго рода равно числу степеней свободы системы.

Уравнения Лагранжа дают единый и достаточно простой метод решения задач динамики и для простых и для сложных механических систем.

При составлении уравнений (7.16) для заданной механической системы рекомендуется следующая последовательность действий:

¾ установить число степеней свободы системы и выбрать обобщенные координаты;

¾ изобразить систему в произвольном положении (обобщенные координаты должны быть положительными) и показать на рисунке все действующие на систему внешние силы;

¾ вычислить кинетическую энергию системы в ее произвольном движении и выразить ее через обобщенные координаты и обобщенные скорости ;

¾ выполнить предусмотренные уравнениями Лагранжа операции дифференцирования кинетической энергии системы;

¾ вычислить обобщенные силы, последовательно задавая элементарные положительные перемещения только соответствующей обобщенной координате;

¾ подставить все полученные выражения в уравнениях Лагранжа и решить полученную линейную систему K уравнений относительно K неизвестных обобщенных ускорений: .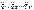

Пример 1. Твердое тело вращается вокруг неподвижной оси z под действием вращающего момента . Составить дифференциальное уравнение вращения твердого тела.

Решение. В качестве обобщенной координаты выберемугол поворота . Соответствующая обобщенная сила равна

Кинетическая энергия вращающегося тела

Уравнение Лагранжа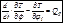

после подстановки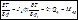

примет вид Это и есть искомое дифференциальное уравнение.

=10.=

Теорема об изменении момента кол-ва движения точки. Закон сохранения момента кол-ва движения МТ.

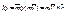
Теорема:

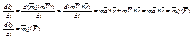
Производная по времени от момента кол-ва движения точки равно моменту силы,действующей на точку относительно того же центра.

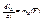
Закон сохранения момента кол-ва движения:

Если , то

Если , то

=13=

Частные случаи динамической теоремы Кориолиса.

1.Переносное вращение не равномерное:

2.Переносное вращение равномерное:

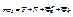
3.Переносное движение поступательное криволинейное:

4.Переносное движение поступательное прямолинейное неравномерное:

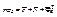
5.Переносное поступательное прямолинейное равномерное:

Принцип относительности классической механики.

Принцип Галилея – не какие механические явления протекающие в среде не могут обнаружить её прямолинейного равномерного поступательного движения.

=14=

Элементарной работой силы Р на бесконечно малом перемещении dr точки, её приложения на скаляное произведение векторов Р и dr: =P*dr/

В координатной форме (Аналитическое выражение работы)

В естественной форме: = 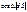элемент работы силы Р, приложенный к твердому телу, вращающемуся вокруг неподвижной оси: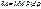

Элементарная работа через обобщённые координаты:

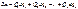
Работа суммы сил равна алгебраической сумме работ, совершённой каждой из сил в отдельности.

Работа равнодействующей(постоянной) силы:

=11=

Относительное движение материальной точки. Переносная и Кориолисова силы инерции.

Движение материальной точки в неинерциальной системе отсчета описывается следующим дифференциальным уравнением, называемым дифференциальным уравнением относительного движения точки

(1.1)

, где - главный вектор активных сил, приложенных к рассматриваемой точке.

- главный вектор реакций связей,

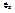- переносная сила инерции,

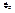- Кориолисова сила инерции.

Уравнение (1.1) отличается от основного уравнения динамики тем, что к действующим на точку активным силам и реакциям связей добавляются переносная и кориолисова силы инерции, связанные с движением точки. Следовательно, относительное движение зависит не только от действующих на точку сил, но и от движения подвижной системы отсчета.
Переносная и кориолисова силы инерции равны произведению массы точки на соответствующее ускорение и направлены противоположно ускорению

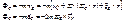
, где - ускорение точки, принятой за полюс, например, начала подвижной системы координат,

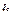, - угловая скорость и угловое ускорение подвижной системы координат,

- радиус-вектор точки в подвижной системе координат,

- относительная скорость.

Дата добавления: 2014-12-16