Принцип Даламбера для М.Т., для механической системы

Понятие о силе инерции.

Даламберова сила инерции - векторная величина, численно равная произведению массы точки на модуль её ускорения.

При криволинейном неравномерном движении точки

Принцип Даламбера для точки – позволяет задачи динамики решать средствами статики.

В каждый момент времени сумма сил активных, сил реакции связи и сил инерции, условно приложенных к точке равна нулю.

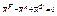
Принцип Даламбера для систем.

Сумма активных сил, сил реакции связи и сил инерции, условно приложенных к точкам системы, а также сумма моментов всех этих сил, относительно любого центра, должны быть равны нулю.

,

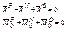Где

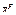-главный вектор активных сил

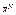- главный вектор сил реакций связи

- главный вектор сил инерции

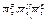- моменты этих сил.

Порядок решения задач.

1.изображаем на схеме акт. силы

2. освобождаемся от связей, прикладываем реакции связей, налож. на каждую точку системы.

3.прикладываем силы инерции.

4. выбираем систему координат.

5. составл. ур-е равновесия для каждой из МТ, решаем систему ур-й.

=26=

Общее уравнение динамики.

Общее уравнение динамики относится к уникальному методу исследования задач динамики механических систем.

Рассмотрим голономную систему N материальных точек, подчиненную идеальным связям. Каждая точка системы движется согласно основному закону динамики

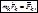
где 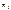– масса k -ой точки системы, 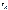– ее ускорение, – равнодействующая внешних сил, приложенных к k –ой точке (k=1,2,…,N).

Если ввести силу инерции 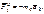то уравнение (6.1) можно записать в форме равновесия сил

Или (6.2)

Выражение (6.2) соответствует принципу Д‘Аламбера: совокупность всех внешних сил, действующих на механическую систему и сил инерции образует в каждый момент времени уравновешенную систему сил.

Мысленно зафиксируем время t и сообщим каждой точке системы одно из возможных перемещений 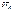Умножим скалярно каждое слагаемое уравнения (6.2) на , затем сложим между собой все N полученных уравнений между собой, получим

т.е. ,

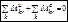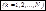6.3)

здесь: 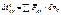– элементарная работа внешних сил, на одном из возможных 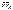перемещений ; – элементарная работа сил инерции на том же возможном перемещении.

Уравнение (6.3) называется общим уравнением динамики:

при движении механической системы в каждый момент времени сумма элементарных работ всех действующих на систему внешних сил и сил инерции на любом возможном перемещении равна нулю.

Так как в уравнение (6.3) входит работа сил инерции, величина которой выражается через ускорение точек системы 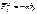, то эти уравнения дают возможность составлять дифференциальные уравнения движения механической системы.

Если механическая система представляет собой абсолютно твердое тело и если это тело движется поступательно, то множество сил инерции точек тела следует заменить главным вектором сил инерции, приложенным к центру масс этого тела и равным

(6.4)

здесь М – масса тела, 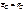ускорение центра масс тела.

Если твердое тело вращается относительно неподвижной оси z, и ось вращения является главной центральной осью, то множество моментов от сил инерции следует заменить главным моментом сил инерции, равным

(6.5)

здесь 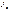– момент инерции тела относительно оси вращения, 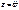– угловая скорость.

Если твердое тело совершает плоское движение, то множество сил инерции всех точек заменяют главным вектором сил инерции, приложенным к центру масс этого тела и главным моментом сил инерции относительно центра.

=25=

Принцип возможных перемещений.

Положением равновесия называется такое положение системы, в котором система будет находиться все время, если в начальный момент времени она находилась в этом положении, и скорости всех ее точек были равны нулю.

Положение системы будет положением равновесия в том случае, когда в этом положении системы (5.1)

Равенство (5.1) выражает принцип возможных перемещений:

для того,чтобы стационарная механическая система с идеальными конечными связями находилась в положении равновесия, необходимо и достаточно, чтобы в этом положении сумма элементарных работ внешних сил на любых возможных перемещениях системы равнялась нулю.

Принцип возможных перемещений был известен со времен Архимеда под названием ˝золотого правила механики˝ и применялся к простейшим механизмам. Рассмотрим в качестве примера рычаг Архимеда Рычаг имеет одну степень свободы – может вращаться вокруг точки О. Равновесие имеет место, когда элементарная работа при повороте рычага на элементарный угол равна нулю.

Имеем

Поэтому 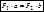или ,

выигрыш в силе компенсируется проигрышем в перемещении и наоборот – золотое правило механики.

Принцип возможных перемещений можно применять для определения реакций опор (реакций связей). Для этого связь, реакцию которой необходимо определить, отбрасывают (освобождают систему от этой связи), заменяя ее силой реакции. Эту силу добавляют к внешним силам. Оставшиеся связи должны быть идеальными. Неидеальную связь заменяют идеальной, компенсируя неидеальность соответствующими силами. Так, если связью тела является шероховатая поверхность, то ее заменяют гладкой поверхностью, добавляя к внешним силам силу трения скольжения.

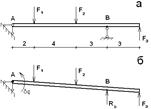
Пример 1. На тело АВ, лежащее на шарнирных опорах А и В, действует нагрузка, как показано на Определить реакцию шарнира В, если F₁=10 кH, F₂=20 кH, F₃=30 кH. Все размеры показаны на рисунке в метрах.

Решение. На заданное тело АВ наложено три связи. Мысленно отбросим шарнирно – подвижную опору В, т. е. одну связь, заменив ее действие искомой реакцией Реакция становится внешней силой. Прикладываем к телу все заданные силы.

Система приобрела одну степень свободы. Теперь на тело наложено две связи. Тело АВ под действием внешних сил будет вращаться в плоскости вокруг шарнира А, возможным перемещением балки будет ее поворот вокруг шарнира А. Повернем балку, например, против хода часовой стрелки на , т. е. зададим системе возможное перемещение.

Запишем принципвозможных перемещений (5.1). Каждое слагаемое в полученном уравнении будет представлять собой элементарную работу, совершаемую соответствующей внешней силой.

Имеем

,

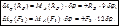
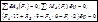отсюда

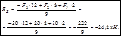
Ответ:

Модуль реакции 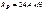, направлена реакция вниз.

=27=

Уравнение Лагранжа 2-го рода

∑δA_i^a+∑δA_i^u=0

Q^a=∑δA^a_i / δq; Q^u=∑δA^u_i / δq следовательно

Q^aδq+Q^uδq=0

(Q^a+Q^u)δq=0; δq не равно 0; следовательно Q^a+Q^u=0

-Q^u=Q^a

Представим обобщенную систему сил, зависящую от сил инерции через массу тел системы, ускорение и возможное перемещение с помощью преобразований получаем уравнение Лагранжа 2-го рода:

d/dt(δT/δq)-δT/δq=Q

Производная по времени от частной производной кинетической энергии до обобщенной скорости минус частная производная кинетической энергии по обобщенной координате равно обобщенной силе.

T-кинетическая энергия системы в ее текущем положении

q-обобщенная координата

q-обобщенная скорость

Q- обобщенная сила системы

Q=∑δA_i / δq

=33=

С кинематической точки зрения удар характеризуется скоротечностью процесса и значительным изменением скорости,при незначительном изменении координаты, с динамической точки зрения, удар характерезуется мгновенным возникновением значительных по величине импульсов.

При ударе необходимо учитывать не только силы вызывающие удар,но и вид движения тел при ударе, а также и материял удоряемого тела.

В простейших случаях удар это практически мгновенное приложение либо снятие связей.

Простейшие виды удара

1) Столкновение 2 тел одно из которых движется поступательно.

2) Отрыв части тела приведший к вращению.

3) Ковка,штамповка забивание сваи

Основной характеристикой при ударе является ударный импульс,

Рассмотрим 2 тела двигающиеся в одном напровлении;

V₁>V₂

V₁-U фаза диформаций, скорость первого тела- V₁¹

V₂-U [1]

Действие ударной силы на материальную точку.

Во время удара как правило силами не ударного характера принебригают.

Теорема об изменении количества движения системы при ударе,для первой точки где,

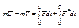
Для? системы применение количества движения системы за некоторый промежуток вренени равно ветторной сумме внешних ударных импульсов приложенных к точкам системы.

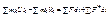
Теорема о изменении количества движения

Изменение момента количества движения системы при ударе,за время удара равно сумме моментов внешних ударных импульсов за то же время

Запишем теорему о изменении момента количества движения

Момент относительно оси z_а и z_b = 0 т.к.эти импульсы пересекают ось

Определение угловой скорости вращения после удара

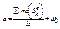
Угловая скорость вращения после удара изменяется на величину ран\вную моменту импульса относительно той же оси.

=34=

Действие ударной силы на материальную точку. Теорема об изменении количества движения материальной точке при ударе.

mU –mV = S

_ _ _

m(U – V)= S

_ _ _

U – V= S

_ _ _

U=S / m +V

Во время удара как правило силами неударного характера пренебрегают.

Теорема:

На некоторую систему материальных точек действуют ударные силы.

Пусть ν_i-скорость до удара

U_i- после удара

Следовательно:

mU_i – mV_i = S_i^e + S_iⁱ

∑mU_i - ∑mV_i = ∑S_i^e + ∑S_iⁱ

∑S_iⁱ=0 следовательно K-K_o=∑S_i^e

K,K_o- количество движения из начального положения в конечное

Изменение количества движения системы при ударе равно геометрической сумме внешних ударных импульсов, действующие на точки системы.

_ _

r_c= ∑m_ir_i / M

_ _

M_rc= ∑r m_i r_i

_{_ _ _ _}

Mdr_c / dt=∑m_i dr_i /dt следовательно MV_c= m_iV_i

_{_ _}

MU_c – MV_c = ∑S^e_i

=35. =

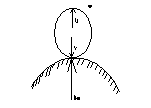
Теорема об изменении кинетического момента механической системы при ударе.

m_kU_k - m_kU_{k =} S^e_k + Sⁱ_k

(r _k×m_kU_k) – (r _k×m_kV_k) = (S^e_k×r _k) + (Sⁱ_k×r _k)

∑(r _k×m_kU_k) – ∑(r _k×m_kV_k) = ∑(S^e_k×r _k) +∑ (Sⁱ_k×r _k)

I – I₀ = ∑m₀(S^e_k) + ∑m₀(Sⁱ_k)

L_z - L_{zo =} ∑m_z(S^e_k)

Если ∑m_z(S^e_k) = 0 то L = const

Изменение момента количества движения системы при ударе за некоторый промежуток времени равно сумме моментов внешних ударных импульсов за тоже время.

=36. =

Теорема об изменении количества движения механической системы при ударе.

Для одной точки

τ τ

mU-mV=∫ Fdt+ ∫F*dt

0 0

F*-сила неударного характера

∑m_kU_k - ∑m_kτ_k=∑Fdt + ∑F*dt

K- K₀=∑S_k

Для идеальной системы изменение количества системы занимает промежуток времени равный векторной сумме внешних ударных импульсов приложенных к точке системы.

K_y –K_0y=∑S^e_ky

Если ∑S^e_kx=0 то kx=const

Если ∑S^e_ky=0 то ky= const

=37=

Запишем теорему об изменении количества движения системы:

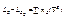; , так как эти импульсы пересекают ось.

,

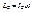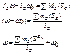
Последняя формула-определение угловой скорости вращения после удара.

Угловая скорость вращения тела после удара изменяется на величину, равную отношению момента ударного импульса к моменту инерции тела относительно той же оси.

Чтобы избежать возникновения ударных реактивных импульсов в опорах, ударный импульс должен быть приложен в центре удара, так как лежащая в плоскости z, a, y, отстоящая оси вращения на расстоянии 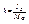, при этом точка К располагается в плоскости 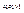, проходящей через точку О, для которой ось z главная ось инерции.

=38=.

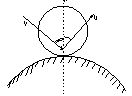
Удар тела о неподвижную поверхность. Линия удара, центральный, косой удар. Коэффициент восстановления при ударе.

Центр масс тела до удара лежит на общей нормали n тела и неподвижной поверхности, скорость v тела до удара направлена по этой нормали (а);

Ударная сила – мгновенная реакция поверхности Nуд.

Удар делится на две фазы:1) от момента прикосновения тела к поверхности до момента полной остановки тела в деформированном состоянии. 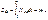m-масса тела: -длительность фазы

2)От конца фазы первой фазы до момента когда тело отделяется поверхности со скоростью u, частично восстанавливая свою форму:

Для скоростей имеется соотношение 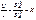- коэффициент восстановления.

Для реальных веществ 0<K<1

=39=

Где V-скорость до удара; U-скорость после удара;

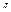-угол до падения; - угол отражения.

По теореме об изменении количества движения:

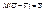
Спроецируем это уравнение на ось тангенсов:

, .

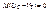Спроецируем тоже уравнение на ось нормалей:

(1)

, подставим V и U в формулу (1) получим:

=40=

В случае абсолютно неупругого удара потери кинетической энергии механической системы равны кинетической энергии системы, если бы её тела двигались с потерянными скоростями:

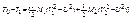, где -скорости тел системы до удара, -скорости тел системы после удара для абсолютно неупругого удара.

Для частично неупругого удара:

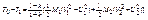, где к- коэффициент упругости.

Для случая когда , то 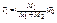, если 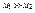, то тело 1 больше по массе (пример: забивка сваи или гвоздя).

тело 2 больше по массе (пример: ковка металла).

=41=

Дата добавления: 2014-12-16