Главный момент сил инерции твердого тела, вращающегося вокруг неподвижной оси

Главный момент сил инерции механической системы

Вычислим главный момент сил инерции системы.

Имеем 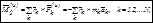(6.12)

так как , (а)

здесь - кинетический момент системы.Подставляя (а) в (6.12), получаем значение главного момента сил инерции 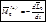(6.13)

Главный момент сил инерции твёрдого тела, вращающегося, вокруг неподвижной оси, сводится к паре сил, момент которого равен 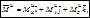(6.14)

где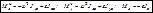

Если ось вращения проходит через центр тяжести тела и оси xyz являются главными осями, то (6.14а)

=17=

Момент инерции тела – характеристика инерции тела для его непоступательного движения.

Момент инерции этой точки относительно оси равен моменту инерции этого тела относительно той же оси.

Момент инерции тела относительно центра оси – плоскости.

-центр

- физический смысл оси; -центр плоскости.

Центробежные моменты инерции- момент инерции, который учитывает неравномерность распределения масс относительно оси. Это единственный момент инерции, который может принимать положительные и отрицательные значения.

, ,

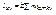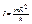
=18=

Радиус инерции()-величина определяемая из соотношения .

Радиус инерции- это расстояние от точки в которой условно сосредоточена масса тела до оси.

Определение моментов инерции тел в простейших случаях:

1)длинный тонкий стержень

2)однородный диск (масса распределена однородна)

Точка распределена по ободу

;

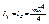
3)однородная пластина

;

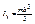=19=

Кинетическая энергия твердого тела. Теорема об изменении кинетической энергии системы

Твердое тело является частным случаем механической системы и рассматривается как непрерывно распределенная масса, тогда все суммы, входящие в выражение для кинетической энергии системы, переходят в интегралы. Так, для твердого тела формула (5.11) примет вид

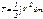. (5.14)

1. Кинетическая энергия твердого тела, двигающегося поступательно.

При этом виде движения скорости всех точек тела одинаковы (рис. 5.8). Вынося в формуле (5.14) за знак интеграла, получим

. (5.15)

Кинетическая энергия твердого тела, движущегося поступательно, равна половине произведения массы тела M на квадрат его скорости.

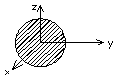
2. Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси

Модуль скорости V любой точки твердого тела, вращающегося вокруг неподвижной оси, равен 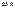, где - модуль угловой скорости твердого тела, - расстояние от точки до оси вращения z (рис. 5.9). Подставляя в формулу (5.14), получим

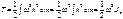(5.16)

здесь 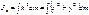– момент инерции твердого тела относительно оси z.

Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.

1. Кинетическая энергия твердого тела при плоско – параллельном движении

При плоско – параллельном движении скорость любой точки тела состоит из геометрической суммы скорости полюса и скорости точки при вращении вокруг полюса. Пусть тело движется плоско в плоскости Oxy, тогда

|| . За полюс выбираем центр масс тела, тогда в формуле (5.13), скорость есть скорость точки k тела при ее вращении относительно полюса (центра масс) и равна , где 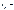расстояние k- ой точки до полюса. Тогда (5.13) перепишется

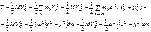
Имея в виду, что 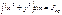– момент инерции тела относительно оси z, проходящей через полюс С, последнее выражение можно переписать как 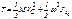(5.17)

при плоско – параллельном движении тела кинетическая энергия складывается из кинетической энергии поступательного движения вместе с центром масс и кинетической энергии от вращения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения.

Дата добавления: 2014-12-16