Закон сохранения движения центра масс

Если главный вектор внешних сил, действующих на систему, равен нулю, т.е. , то из (3.6) следует, что ускорение центра масс равно нулю, следовательно, скорость центра масс 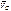является постоянной по модулю и направлению. Если, в частности, в начальный момент центр масс находится в покое, то он покоится в течение всего времени, пока главный вектор внешних сил равен нулю.

Из этой теоремы вытекает несколько следствий.

· Одними внутренними силами нельзя изменить характер движения центра масс системы.

· Если главный вектор внешних сил, действующих на систему, равен нулю, то центр масс находится в покое или движется равномерно и прямолинейно.

· Если проекция главного вектора внешних сил системы на некоторую неподвижную ось равна нулю, то проекция скорости центра масс системы на эту ось не изменяется.

· Пара сил, приложенная к твердому телу, не может изменить движение его центра масс (она может вызвать только вращение тела вокруг центра масс).

Рассмотрим пример, иллюстрирующий закон сохранения движения центра масс.

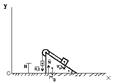Пример 3. Два груза массами и 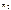соединены нерастяжимой нитью, переброшенной через блок, закрепленный на клине массой М. Клин опирается на гладкую горизонтальную плоскость. В начальный момент система находилась в покое. Найти перемещение клина по плоскости при опускании первого груза на высоту Н. Массой блока и нити пренебречь.

Решение. Внешними силами, действующими на клин вместе с грузами, являются силы тяжести , 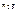и Mg, а также нормальная реакция гладкой горизонтальной поверхности N. Следовательно,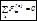

Поскольку в начальный момент система находилась в покое, имеем .Вычислим координату центра масс системы 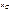при и в момент t₁, когда груз весом g опустится на высоту H.

Для момента : где , , х – соответственно координаты центра масс грузов весом g, 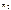g и клина весом Мg.

Предположим, что клин в момент времени 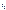переместится в положительном направлении оси Ox на величину L, если груз весом опустится на высоту Н. Тогда, для момента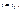

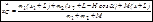
т.к. грузы вместе с клином передвинутся на L вправо, a груз 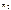переместится на расстояние по клину вверх. Так как , то после вычислений получим 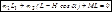, откуда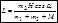

.

=7=

Вторая задача динамики. Постоянные интегрирования, их определения по начальным условиям.

По имеющийся известной массе точки и действующей на точку сил определить уравнение движения точки.

∑x_i=mx =0; x=C₁=0, x=C₁t+C₂ ∑y_i=my =0; y=C₃, y=C₃t+C₄

∑z_i=-mg=mz; z=-gt+C_5, z=-gt²/2+C₅t+C₆

1) при t=0 x₀=C₁=0

x₀=C₂=0

2) y₀=V₀cosα=C₃

y₀=C₄=0

3) z₀ = V₀sinx=C₅

z₀=C₆=0

y=V₀cosαt уравнение траектории

z=-gt² / 2+V₀sinαt в параметрическом виде

t=y / V₀cosα

z= - g (V₀cosα)² / 2+V₀sinx

z= -g/2 (y/ V₀cosα)²+ V₀sinαy / V₀cosα

z=f(y)

=8.=

Теорема об изменении кол-ва движения системы. Закон сохранения кол-ва движения системы.

К- кол-во движения системы.

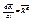- теорема в дифференциальной форме

Проинтегрируем:

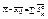- теорема в интегральной форме.

Изменение кол-ва движения системы за некоторый промежуток времени равно сумме импульсов всех внешних сил, действующих на точку, и системы за тот же промежуток времени.

Следствие(Закон сохранения):

если ,то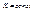

если 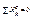,то 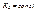и т. п.

Эта теорема лежит в основе расчетов по гидроаэродинамике, теории удара.

=9=

Идеальные связи.Обозначим силы реакций связей системы .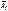

Связи системы называются идеальными, если сумма элементарных работ реакций этих связей на любых возможных перемещениях всегда равна нулю, т. е.

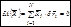(4.1)

Приведем примеры идеальных связей:

1. В абсолютно твердом теле точки связаны идеальными связями. Силами реакций связей в этом случае являются внутренние силы, для которых было доказано, что сумма элементарных работ этих сил на любом возможном перемещении, равна нулю.

2. Абсолютно гладкая поверхность является идеальной связью для точки. Возможные перемещения точки направлены по касательной к поверхности, а силы реакции в этом случае направлены по нормали к ним, т.е. перпендикулярны перемещениям, см. рис.11, следовательно, элементарная работа силы реакции на перемещении равна нулю.

Дата добавления: 2014-12-16