Однородный стержень

Имеем однородный стержень длиной L и массой М. Вычислим момент инерции стержня относительно оси Сz, проходящей через центр масс стержня и перпендикулярной к нему (рис. 2.7).

Для этого нужно просуммировать все массы, умноженные на квадраты расстояния x до оси Cz. Тогда, согласно(2.7), имеем

Если разделить стержень на отрезки длиной dx, то соответствующий элемент массы будет пропорционален dx (dmdx), а если бы dx составляло длину всего стержня, то его масса была бы равна М (M L). Поэтому

Вычисляя интеграл, получаем

Таким образом,

Размерность момента инерции всегда равна массе, умноженной на квадрат длины (кг м²), так что единственная величина, которую мы вычислили, это множитель 1/12.

Момент инерции стержня относительно оси , проходящей перпендикулярно стержню через его конец, параллельно zС, определяется по теореме Гюйгенса-Штейнера: , где

Следовательно

=3=

3.Дифференциальное уравнение движения свободной и несвободной материальной точки в координатной и естественной форме.

Дифференциальное уравнение движения материальной точки.

Рассмотрим движение материальной точки по отношению к инерциальной системе отсчёта под действием системы сил

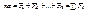-свободная материальная точка.

-несвободная материальная точка.

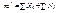
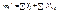-эти 3 уравнения- дифференциальные уравнения движения

материальной точки в координатной форме.

-эти 3 уравнения- дифференциальные уравнения движения для

свободной материальной точки.

Проекция на оси естественного трёхгранника

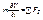- эти два уравнения – дифференциальные уравнения материальной

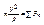точки на оси естественного трёхгранника.

; - тангенсальная и нормальная составляющая ускорения.

ПОМЕТКА: на рисунке везде векторы, где Аr - и т. д.

=4=

Теорема об изменении кол-ва движения точки. Закон сохранения кол-ва движения МТ.

Кол-во движения точки ­­­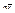- - одна из двух мер механического движения– импульс силы - характеристика действующих сил на точку за некоторый промежуток времени.

Элементарный импульс:

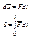
Второй закон Ньютона:

- теорема в дифференциальной форме.

Производная по времени от кол-ва движения точки равна силе,действующей на точку.

- теорема в интегральной форме.

Изменение кол-ва движения точки за некоторый промежуток времени равно импульсу силы, действующей на точку за некоторый промежуток времени

Закон сохранения кол-ва движения:

Если , то

если , то и т. п.

=5=

5.Две задачи динамики. Пример решения первой задачи динамики.

Первая задача динамики:

Зная массу точки и уравнение её движения определяют силы действующие на точку.

Решается эта задача – дифференцированием.

Вторая задача динамики, основная и обратная:

По имеющимся и известной массе точки и действующей на точку силе определить уравнение движения точки.

Решается эта задача – интегрированием.

Пример решения первой задачи динамики:

Законы движения:

Затем дифференцируем эти уравнения:

, так как 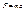- по второму закону Ньютона, то

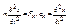
, значит общая сила действующая на эту точку равна:

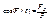, , где - единичный орт по оси х.

В естественной форме:

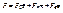
=6=

Теорема о движении центра масс

Известно, что твердое тело и механическая система в плоскости может двигаться достаточно сложно. К первой теореме о движении тела и механической системы можно прийти следующим образом: бросить к.-л. предмет, состоящий из множества скрепленных между собой твердых тел. Ясно, что он полетит по параболе. Это выявилось при изучении движения точки. Однако теперь объект не точка. Он поворачивается, покачивается в процессе полета вокруг некого эффективного центра, который движется по параболе. Первая теорема о движении сложных предметов говорит о том, что некий эффективный центр есть центр масс движущегося предмета. Центр масс не обязательно находится в самом теле, он может лежать и где-то вне его. Теорема. Центр масс механической системы движется как материальная точка массой равной массе всей системы, к которой приложены все внешние силы, действующие на систему

Для доказательства теоремы перепишем дифференциальные законы движения (3.3) в следующем виде: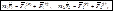

(3.5)

где N – число точек системы.

Сложим почеленно уравнения между собой: 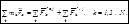(а)

Положение центра масс механической системы относительно выбранной системы координат определяется формулой (2.1): где М – масса системы. Тогда левая часть равенства (а) запишется (б)

Первая сумма, стоящая в правой части равенства (а), равна главному вектору внешних сил, а последняя по свойству внутренних сил равна нулю. Тогда равенство (а), с учетом (б) перепишется (3.6)т.е. произведение массы системы на ускорение центра ее массы равно геометрической сумме всех действующих на систему внешних сил.

Из уравнения (3.6) следует, что внутренние силы непосредственно не влияют на движение центра масс. Однако в ряде случаев являются причиной появления внешних сил, приложенных к системе. Так, внутренние силы, приводящие во вращение ведущие колеса автомобиля, вызывают действие на него внешней силы сцепления, приложенной к ободу колеса.

Пример 2. Механизм, расположенный в вертикальной плоскости, установлен на горизонтальной гладкой плоскости и прикреплен к ней жестко закрепленными с поверхностью брусками К и рис.

Диск 1 радиусом R неподвижен. Диск 2 массой m и радиусом r скреплен с кривошипом , длиной R+r в точке С₂. Кривошип вращается с постоянной

угловой скоростью . В начальный момент кривошип занимал правое горизонтальное положение. Пренебрегая массой кривошипа, определить наибольшее горизонтальное и вертикальное усилия, действующие на бруски, если общая масса станины и колеса 1 равна М. Также рассмотреть поведение механизма при отсутствии брусков.

Решение. Система состоит из двух масс (N=2): неподвижного диска 1 со станиной и подвижного диска 2. Направим ось у через центр тяжести неподвижного диска по вертикали вверх, ось х – вдоль горизонтальной плоскости.

Запишем теорему о движении центра масс (3.6) в координатной форме (б)Внешними силами этой системы являются: вес станины и неподвижного диска – Mg, вес подвижного диска – mg, - суммарная горизонтальная реакция болтов, - нормальная суммарная реакция плоскости. Следовательно, 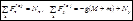(в)

Тогда законы движения (б) перепишутся

Вычислим координаты центра масс механической системы:

(г)

как видно из рис., , , (угол поворота кривошипа ), . Подставляя эти выражения в (г) и вычисляя вторые производные по времени t от 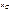, , 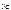получим, что (д)

Подставляя (в) и (д) в (б), находим

Горизонтальное давление, действующее на бруски, имеет наибольшее и наименьшее значения, когда cos = 1 соответственно, т.е

Давление механизма на горизонтальную плоскость имеет наибольшее и наименьшее значения, когда sin 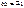соответственно, т.е.

Фактически решена первая задача динамики: по известным уравнениям движения центра масс системы (д) восстанавливаются силы, участвующие в движении.

В условиях отсутствия брусков K и L рис, механизм может начать подпрыгивать над горизонтальной плоскостью. Это будет иметь место, когда 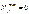, т.е. когда , отсюда следует, что угловая скорость вращения кривошипа, при которой происходит подпрыгивание механизма, должна удовлетворять равенству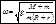

Дата добавления: 2014-12-16