
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вынужденные колебания механической системы без учета сил сопротивления
|
|
|
|
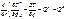

Возможны 2 случая:
 и
и 
1) 

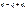

 - решение будем искать в виде правой части
- решение будем искать в виде правой части
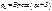
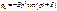
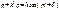

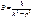
 - уравнение вынужденных колебаний без учета сил сопротивления.
- уравнение вынужденных колебаний без учета сил сопротивления.
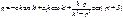
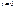 ,
, 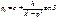
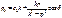
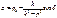

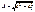

2) 

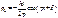


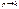

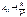


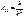
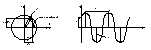
 - Амплитуда.
- Амплитуда.
Малые свободные колебания механической системы. (собственные)
Колебательное движение – движение, при котором одна или несколько обобщенных координат периодически принимают нулевые значения. Причиной малых свободных колебаний служат: начальное отклонение или придание объекту начальной скорости.
Устойчивость. Положение механической системы может быть равновесным или нет. В свою очередь положение равновесия может быть устойчивым, неустойчивым и безразличным.
Устойчивое положение – когда при малом изменении обобщенной координаты тело стремится занять исходное положение.
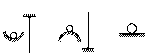 1 – устойчивое положение;
1 – устойчивое положение;
2 – неустойчивое;
3 – безразличное.
Устойчивость положения определяется теоремой Лагранжа-Де-Рихле, которая носит достаточный характер.
В положении равновесия все обобщенные координаты имеют нулевое положение и их отсчет ведут от этого положения.
Теорема: для того, чтобы механическая система с голономными идеальными связями находилась в равновесии, достаточно чтобы первая четная производная потенциальной энергии по обобщенной координате была > 0.
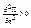 - устойчивое положение системы.
- устойчивое положение системы.
Собственные колебания.
Малые свободные колебания всегда линейны. Малые – когда величины малы q, q’,q”, при этом в уравнении Лагранжа эти величины 2-го порядка и выше отбрасываются и колебания всегда описываются линейными уравнениями.
Рассмотрим колебания механической системы с идеальными связями, имеющей одну степень свободы и описанной одним уравнением Лагранжа:
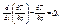

В общем случае структура обобщенной силы складывается из части, зависящей от действия потенциальных сил, сил сопротивления и возмущенных сил.
Рассмотрим механическую систему с консервативными силами:
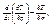
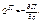
Для решения уравнения Лагранжа нужно определить кинетическую энергию системы в виде:
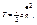 а – коэффициент инерции системы, зависит от размерности обобщенной координаты.
а – коэффициент инерции системы, зависит от размерности обобщенной координаты.
Потенциальную энергию ищут в виде: 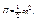 с – коэффициент жесткости системы.
с – коэффициент жесткости системы.
Произведем действия в соответствии с уравнением Лагранжа:



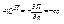
Подставим полученные выражения в уравнение Лагранжа:

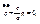
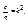

k – циклическая частота колебаний.
В результате уравнение Лагранжа приводиться к дифференциальному уравнению 2-го порядка, однородному без правой части, линейному.
Решение дифференциального уравнения приводится к уравнению, зависящего от корней характеристического уравнения:
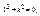
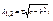
 то решается в виде:
то решается в виде: 
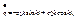
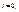

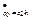

 - решение диф. уравнения.
- решение диф. уравнения.
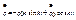 - обобщенная скорость.
- обобщенная скорость.
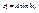

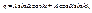
 - решение дифференциального уравнения в амплитудной форме, где: А – амплитуда колебаний;
- решение дифференциального уравнения в амплитудной форме, где: А – амплитуда колебаний;
α – начальная фаза колебаний; k – частота колебаний; 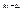 - фаза колебаний;
- фаза колебаний;
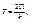 - период колебаний.
- период колебаний.
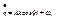 при t=0:
при t=0: 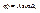




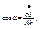
 - уравнение эллипса.
- уравнение эллипса. 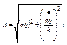
Графически можно интерпретировать как семейство эллипсов, построенных в фазовой плоскости
с осями q и q’. Если система совершает гармонические колебания, то эллипсы замкнуты, а их вид зависит от начальных условий.
Основные свойства малых свободных колебаний:
1) Они гармонические;
2) Амплитуда и начальная фаза определяются начальными условиями;
3) Точки системы движутся периодически, проходя положение равновесия;
4) Все точки системы движутся в одной фазе, одновременно достигая положения равновесия.
5) Малые свободные колебания изображаются семейством эллипсов в фазовой плоскости.
Содержание:
1.Предмет динамики. Масса материальной точки. Сила Закона динамики. Инерциальные системы отсчёта.
2.Теорема Штейнера-Гюйгенса-Эйлера о моментах инерции относительно параллельных осей. Примеры вычисления моментов инерции.
3.Дифференциальное уравнение движения свободной и несвободной материальной точки в координатной и естественной форме.
4.Теорема об изменении количества движения точки. Закон сохранения количества движения материальной точки.
5.Две задачи динамики. Пример решения первой задачи динамики.
6.Теорема о движении центра масс системы. Закон сохранения движения центра масс.
7.Вторая задача динамики. Постоянные интегрирования, их определение по начальным условиям.
8.Теорема об изменении количества движения системы. Закон сохранения количества движения системы.
9.Идеальные связи. Обобщённые силы. Вычисление обобщённых сил.
10.Теорема об изменении количества движения точки. Закон сохранения момента количества движения.
11.Относительное движение материальной точки. Дифференциальные уравнения относительного движения материальной точки. Переносная и Кориолисова силы инерции.
12.Теорема об изменении количества движения системы. Закон сохранения кинетического момента системы.
13.Частные случаи динамической теоремы Кориолиса. Принцип относительности классической механики.
14.Работа силы. Работа равнодействующей силы. Аналитическое выражение работы.
15.Работа силы тяжести. Работа упругой силы. Работа силы приложенной к телу, имеющему оси вращения.
16.Механическая система. Масса, центр масс системы. Внешние и внутренние силы системы. Момент инерции твёрдого тела относительно центра, оси, плоскости.
17.Момент инерции твёрдого тела относительно центра, оси, плоскости. Центробежные моменты инерции.
18.Понятие о радиусе инерции. Определение моментов инерции тел в простейших случаях.
19.Кинетическая энергия твёрдого тела в различных случаях его движения. Теорема об изменении кинетической энергии механической системы.
20.Потенциальное силовое поле. Потенциальная функция. Поверхность равного потенциала. Работа силы в потенциальном поле.
21.Потенциальная энергия. Закон сохранения механической энергии.
22.Связи и их уравнения. Квалификация связей. Обобщённые координаты. Возможные перемещения.
23.Приведение сил инерции к центру. Главный вектор и главный момент инерции.
24.Принцип Даламбера для материальной точки, для механической системы.
25.Принцип возможных перемещений. Пример.
26.Общее уравнение динамики.
27.Уравнение Лагранжа 2-ого рода.
28.Понятие об устойчивости механической системы. Теорема Лагранжа-Дирихле.
29.Собственные малые колебания системы. Амплитуда, период, начальная фаза колебаний. Явление резонанса.
30.Малые колебания механической системы с учётом линейного сопротивления.
31.Вынужденные колебания механической системы без учёта сил сопротивления.
32.Вынужденные колебания механической системы с учётом сил сопротивления.
33.Теория удара, общие положения. Ударный импульс.
34.Действие ударной силы на материальную точку. Теорема об изменении количества движения материальной точки при ударе.
35.Теорема об изменении кинетического момента механической системы при ударе.
36.Теорема об изменении количества движения механической системы при ударе.
37.Действие ударных сил на тело, вращающееся вокруг оси.
38.Удар тела о неподвижную поверхность. Линия удара, центральный, косой удар. Коэффициент восстановления при ударе.
39.Косой центральный удар.
40.Теорема Карно.
41.Равновесие системы тел.
42.Сложное движение точки. Модуль и направление ускорения Кориолиса.
43.Фермы. Определение усилий в стержнях фермы.
44.Плоскопараллельное движение твёрдого тела. Определение скорости точки тела в плоском движении методом полюса и методом МЦС.
=1=
Предмет динамики, масса материальной точки. Сила закона динамики. Инерциальная система отчета.
Динамика-раздел теор. мех., в которой изучают движение тел или систем тел с учетом их масс и под действием приложенных сил. Все задачи в динамики сводятся к рассмотрению 2-х задач:
1) прямая задача динамики- то есть по известным кинематическим параметрам определяют приложенные к этой точке силы.
x=x(t) x =ax
y=y(t) y =ay
z=z(t) z =az
md2x/dt2=Fx
md2y/dt2=Fy F√(Fx2+F2y+F2z)
md2z/dt2=Fz
2)Обратная задача динамики- когда по известной массе точки и действующей на точку сил определяют уравнение движения точки.
∑xi=mx =0 x=C1=0, x=C1t+C2
∑yi=my =0 y=C3, y=C3t+C4
∑zi=-mg=mz z=-gt+C5, z=-gt2/2+C5t+C6
Масса материальной точки- это величина прямопропорциональная его весу и обратно ускорению свободного падения.
Материальная точка- это такая точка, размерами которой можно пренебречь.
Инерциальная система отчета- это система, в которой выполняется закон инерции. За инерциальную систему отчета принимают систему отчета связанную с Землей.
Система отчета- это система координат, по отношению к которой движется точка.
Сила- это мера механического взаимодействия тел, определяющее интенсивность и направление этого взаимодействия.
Постоянные силы F=const, направленные силы тяжести в близи поверхности земли.
Переменные силы зависят от положения точки F=f(r)- сила упругости
1) от времени F=f(t)
2) от скорости F=f(dr/dt)
Законы динамики:
1) Закон инерции: материальная точка находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит его движение.
2) Закон пропорциональности силы и ускорения: ускорение материальной точки пропорционально силе, приложенной к ней и движется с ней в одинаковое направление.
3) Закон действия и противодействия или равенства: два тела взаимодействуют с силами равными по модулю и направленными вдоль одной прямой противоположно направлению
4) Закон независимости действия сил: если на точку действует система сил, то ускорение которое они ей сообщают равно геометрической сумме ускорений сообщаемых каждой из сил в отдельности.
=2=
Теорема Штейнера-Гюйгенса-Эйлера о моментах инерции относительно параллельных осей. Примеры вычисления моментов инерции.
Существует простая связь между моментами инерции тела относительно параллельных осей (теорема Гюйгенса-Штейнера), одна из которых проходит через центр масс.
Теорема. Момент инерции тела 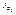 относительно некоторой оси
относительно некоторой оси  равен сумме момента инерции
равен сумме момента инерции  тела относительно оси
тела относительно оси 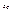 проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояний между осями:
проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояний между осями: 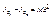 (1)
(1)
где М – масса тела, d – расстояние между двумя параллельными осями.
Пусть оси  и
и 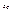 параллельны, причем ось
параллельны, причем ось 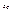 проходит через точку С – центр масс тела.
проходит через точку С – центр масс тела.
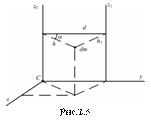
Возьмем начало координат в точке С, совместим ось zс осью 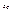 , а ось у направим так, чтобы она пересекала оси
, а ось у направим так, чтобы она пересекала оси  и
и 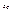 (рис.2.5)
(рис.2.5)
Выделим в теле произвольный элемент массой dm и опустим из него перпендикуляры на оси z и  , обозначив их соответственно h и
, обозначив их соответственно h и 
Согласно определению осевых моментов инерции моментов, будем иметь
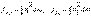
По теореме косинусов (рис.2.5) найдем 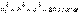 , однако
, однако 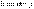 , где у – координата элемента, тогда
, где у – координата элемента, тогда 
Подставим полученное выражение 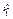 в формулу (1), определяющую момент инерции
в формулу (1), определяющую момент инерции 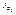
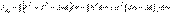
Первый интеграл равен 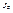 по определению, второй – массе тела М, а третий – нулю:
по определению, второй – массе тела М, а третий – нулю:  , поскольку начало координат совпадает с центром масс. Следовательно,
, поскольку начало координат совпадает с центром масс. Следовательно, 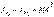
Получим формулы для вычисления моментов инерции некоторых простых тел.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 1111; Нарушение авторских прав?; Мы поможем в написании вашей работы!