Теорема об изменении кинетической энергии системы

Пусть точки системы массой 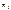переместились так, что их радиус-векторы в инерциальной системе отсчета получили приращение . Найдем, как при этом изменилась кинетическая энергия Т системы.

Согласно (5.11), кинетическая энергия системы

.Вычислим дифференциал кинетической энергии системы и преобразуем полученное выражение

здесь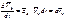

Принимая во внимание, что 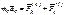, где - ускорение точки а и 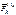- равнодействующие внешних и внутренних сил, приложенных к точке, перепишем последнее равенство в виде

.

Таким образом, (5.23)

Последнее равенство выражает теорему об изменении кинетической энергии механической системы в дифференциальной форме: дифференциал кинетической энергии системы равен элементарной работе всех сил системы.

Частный случай. Для абсолютно твердого тела сумма работ всех внутренних сил системы равна нулю: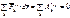

.Следовательно, теорему об изменении кинетической энергии (5.23) для твердого тела можно записать в виде 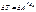(5.24)

Изменение кинетической энергии твердого тела при каком-либо элементарном перемещении равно элементарной работе внешних сил, действующих на тело.

Если обе части (5.24) проинтегрировать между двумя положениями – начальным и конечным, в которых соответственно кинетическая энергия 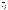и , получаем (5.25)

=20. =

Потенциальное силовое поле. Потенциальная функция. Поверхность равного потенциала. Работа силы в потенциальном поле.

Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке. Примером может служить поле силы тяжести Земли или поле сил сопротивления в потоке жидкости (газа). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы.

Работа, которую совершают силы поля при перемещении частицы из точки 1 в точку 2, зависит, вообще говоря, от пути. Однако среди стационарных силовых полей имеются такие, в которых эта работа не зависит от пути между точками 1 и 2. Этот класс полей, обладая рядом важнейших свойств, занимает особое место в физике. Рассмотрим свойства таких полей.

Введем определение: стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называется потенциальным, а сами силы - консервативными.

Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными. К числу таких сил принадлежит, например, сила трения, так как работа этой силы зависит в общем случае от пути.

Покажем, что в потенциальном поле работа сил поля на любом замкнутом пути равна нулю. Действительно, любой замкнутый путь (рис. 5.5) можно разбить произвольно на две части: 1а2 и 2b1. Так как поле

потенциально, то, по условию 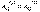С другой стороны, очевидно, что Поэтому

что и требовалось доказать.

Наоборот, если работа сил поля на любом замкнутом пути равна нулю, то и работа этих сил на пути между произвольными точками 1 и 2 от формы пути не зависит, т. е. поле потенциально. Для доказательства выберем два произвольных пути: 1а2 и 1b2 (рис. 5.5). Составим из них замкнутый путь 1a2b1. Работа на этом замкнутом пути по условию равна нулю, т. е. 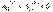Отсюда Но , поэтому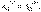

Таким образом, равенство нулю работы сил поля на любом замкнутом пути есть необходимое и достаточное условие независимости работы от формы пути, и может считаться отличительным признаком любого потенциального поля сил.

Рассмотрим важный случай поля центральных сил. Всякое силовое поле вызывается действием определенных тел. Сила, действующая на частицу А в таком поле, обусловлена взаимодействием этой частицы с данными телами. Если силы, зависят только от расстояния между взаимодействующими частицами и направлены по прямой, соединяющей эти частицы, от их называют центральными. Такими примерами служат силы гравитационные, кулоновские и упругие.

Центральную силу, действующую на частицу А со стороны частицы В, можно представить в общем виде: ,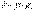

где -функция, зависящая при данном характере взаимодействия только от r - расстояния между частицами; 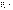единичный вектор, задающий направление радиус-вектора частицы А

относительно частицы В

Докажем, что всякое стационарное поле центральных сил потенциально. Для этого найдем работу центральных сил в случае, когда силовое поле вызвано наличием одной неподвижной частицы B, а затем обобщим результат на произвольный случай. Элементарная работа силы (5.8)

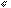на перемещении есть Так как проекция вектора на вектор , или на соответствующий радиус-вектор (рис. 5.6), то Работа же этой силы на произвольном пути от точки 1 до точки 2

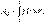
Полученное выражение зависит, очевидно, только от вида функции , т. е. от характера взаимодействия и от значений и 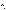- начального и конечного расстояний между частицами A и B. От формы пути оно никак не зависит. Это и означает, что данное силовое поле потенциально.

Обобщим полученный результат на стационарное силовое поле, вызванное наличием совокупности неподвижных частиц, действующих на частицу A с силами 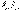.., каждая из которых является центральной. В этом случае работа результирующей силы при перемещении частицы A из одной точки в другую равна алгебраической сумме работ отдельных сил. А так как работа каждой из этих сил не зависит от формы пути, то и работа результирующей силы от нее также не зависит. Таким образом, действительно, любое стационарное поле центральных сил потенциально.

Введем понятие потенциальной энергии частицы в поле. То, что работа сил потенциального поля зависит только от начального и конечного положений частицы, дает возможность ввести чрезвычайно важное понятие потенциальной энергии.

Представим себе, что мы перемещаем частицу в потенциальном поле сил из разных точек P в фиксированную точку O. Так как работа сил поля не зависит от формы пути, то остается зависимость ее только от положения точки P (при фиксированной точке O). А это значит, что данная работа будет некоторой функцией радиус-вектора r точки P.

Обозначив эту функцию 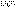, запишем

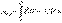Функцию 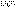называют потенциальной энергией частицы в данном поле.

=21=

Потенциальная энергия. Закон сохранения механической энергии.

Потенциальная энергия – это функция координат точек системы, она представляет собой работу сил поля по перемещению механической системы.

Через каждую точку поля можно провести одну эквипотенциальную поверхность.

При движении механической системы в потенциально-силовом поле полная энергия системы величина постоянная.

Потенциальная энергия материальной точки равна работе сил потенциального поля при переходе из данного положения в нулевое П=-U

=22.=

Квалификация связей.

Свободное тело-перемещение которого ничем не ограничено.

Связи- ограничения, накладываемые на возможные перемещения (скорости) различных тел. Как правило связи- это физические тела.

Связи: голономные связи – накладывают ограничение на положение точки, описавыется уравнением f(x₁y₁z₁)=0. Неголономные – накладывают ограничение на положение точки и её скорость, описываются уравнением f(x₁y₁z₁x^’₁y^’₁z^’₁)=0

Удерживающие связи допускают не только прямое, но и обратное перемещение.

Например стержень(двусторонние).

Неудерживающая(односторонняя). Н-р нить.

Ур-ие удерживающей связи: f(x;y;z)=0

Неудерживающие связи описывается уравнением f(x;y;z)*принадлежит*0

Стационарные связи: в Ур-ия которых время в явном виде не входит.

Геометрические связи: связи, Ур-ия которых содержат координаты точек.

Кинематические связи содержат координаты и скорость.(накладывают ограничения на положение тела и его скорость)

Идеальные связи: такие, работа р-ий которых на бесконечно малых возможных перемещениях равна 0

Например: гладкая поверхность, шарнир без трения и зазоров.

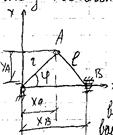
Обобщённые координаты, независимые между собой параметры q_i (r = 1, 2,..., s) любой размерности, число которых равно числу s степеней свободы механич. системы и которые однозначно определяют положение системы. Закон движения системы в О. к. даётся s уравнениями вида q_i = q_i (t), где t — время. О. к. пользуются при решении многих задач, особенно когда система подчинена связям, налагающим ограничения на её движение. При этом значительно уменьшается число уравнений, описывающих движение системы, по сравнению, например, с уравнениями в декартовых координатах. В системах с бесконечно большим числом степеней свободы (сплошные среды, физические поля) О. к. являются особые функции пространственных координат и времени, называются потенциалами и т.п.

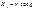
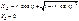
=23=

Главный вектор и главный момент инерции.

К системе сил инерции действующих на систему материальных точек или твёрдое тело применим принцип Пуансо и приведём их к некоторому центру, при этом получим главный вектор сил инерции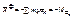

и главный момент инерции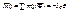

Приведение сил инерции к центру:

1)поступательное движение твёрдого тела. Силы инерции приводятся только к главному вектору (для точки С) и приложенному к центру масс.

2)вращательное движение плоской фигуры вокруг оси перпендикулярной плоскости фигуры:

, ,

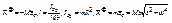
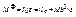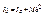
3)плоско - параллельное движение. Силы инерции приводятся к главному вектору приложенному к данному привидению и к главному моменту сил инерции.

На предыдущем рисунке в точке О: , ,если при вращательном движении центр масс совпадает с осью вращения, то , а главный момент: .

=24.=

Дата добавления: 2014-12-16