Частотные критерии качества

Косвенные методы оценки качества

Прямые показатели качества системы

Требования устойчивости для систем не являются достаточной. Необходимо чтобы система имела определенный переходной процесс (частотные свойства), а ее ошибка σ в установившемся режиме не превышала заданной.Вид переходного процесса в общем случае зависит от начальных условий и возмущающего воздействия.

Для большинства систем рассматривается реакция на единичный скачок то есть переходную характеристику

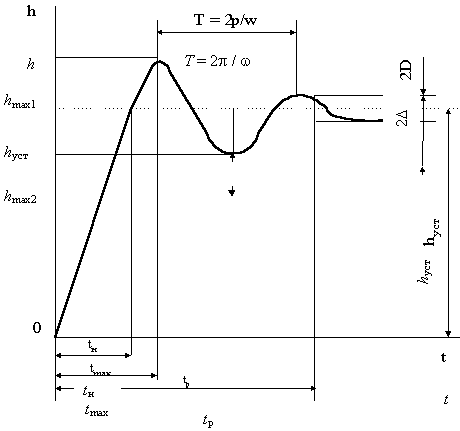
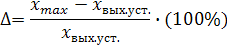
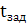-известное время задержки

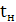-время нарастания

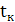-первое время регулирования

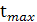-время достижения максимума

Ε-отношения,управляемой величины от установившегося режима

Оценка распределения нулей и полюсов

Частотный метод

Интегральный метод

При анализе устойчивости САР обычно рассматривается ее характеристики в разомкнутом состоянии.

При анализе качества переходных процессов используются частотные характеристики замкнутой системы

Пускай замкнутая система имеет функцию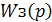

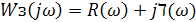
– единичный скачок

Интеграл Фурье выглядит так:

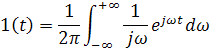
Единичная функция может быть представлена как бесконечный сумма элементарный колебаний

Реакция системы на единичный скачок

(€)

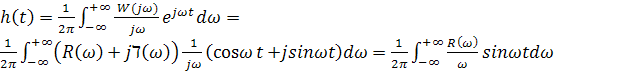По выражению (€) можно определить переходную функцию замкнутой системы

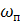- частота положительности

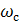- частота существенности

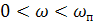
АЧХ - положительна интервал положительный

- диапазон существенности

Обычно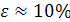

Поскольку 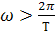,то для ВЧХ область низких частот (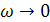) описывает поведения системы в установившемся режиме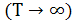

Область В.Ч. (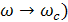 описывает поведения системы в начале переходного процесса,эта область обычно отбрасывается так как ее влияние на качество не существенно.

По анализу выражения (€) установлено:

 

         

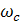
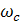
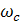
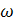
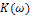
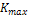
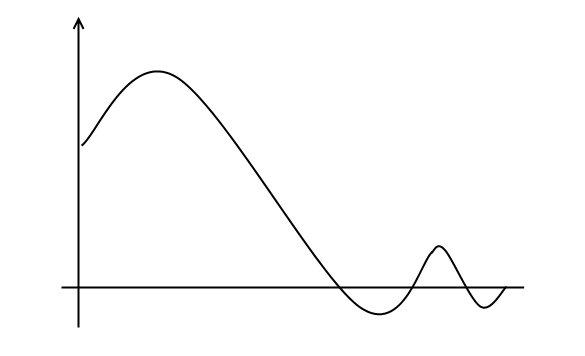Чтобы перерегулирования переходного процесса не превышало 18% достаточно иметь положительную не возрастающую ВЧХ

Чтобы переходной процесс был монотонный необходимо что бы производная АЧХ по 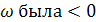и убывала по модулю

Если ВЧХ имеет максимум 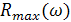то перерегулирования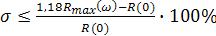

Если ВЧХ имеет интервал положительности 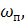то погрешности переходного процесса 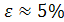в общем случае время регулирования 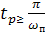для колебательных процессов.Для монотонных и апериодических процессов 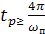.Апериодический и монотонный процессы в 4 раза продолжительней,чем колебательный. Переходной процесс делают иногда колебательным с ограниченным перерегулированием

Изменения масштаба в К- раз по оси 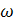вызывает изменения в единицу на К- раз по оси времени для переходного процесса,то есть узким ВЧХ соответствует длительные переходные процессы и наоборот. Изменения масштаба по оси 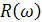ВЧХ соответствует такому же изменению масштаба переходного процесса

Конечное значения переходной функции равно начальному значению ВЧХ

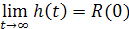
начальное значения переходной функции ровно конечному значению ВЧХ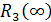

Дата добавления: 2014-12-16