Использование неравенства Чебышева для оценки риска

Возвращаясь к вариации как к мере риска, следует заметить, что дисперсия позволяет в некоторых случаях выявить граничные шансы инвестора. Теоретическая база этого заложена в известном неравенстве Чебышева: вероятность того, что случайная величина х отклоняется по модулю от своего математического ожидания больше, чем заданная величина ε, не превышает ее дисперсии, деленной на ε², или

.

При этом дисперсия некоторой случайной величины х должна быть меньше, чем ε², поскольку вероятность р £ 1.

Это неравенство позволяет находить верхнюю границу вероятности того, что случайная величина х отклоняется (в обе стороны) от своего среднего значения на величину, большую ε.

Здесь - дисперсия случайной величины, вычисляемая по формуле: .

неравенство Чебышева может быть записано и следующим образом:

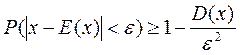
Если нас интересует вероятность отклонения только в одну сторону, например, в большую, то неравенство Чебышева запишется в виде:

.

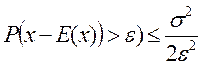Пример 8. У банка имеются должники, значения RNK у которых за три прошедших месяца составили: у первого – 1,5, 1,3, 1,7; у второго – 1,6, 1,4, 1,5. Какова вероятность того, что они в течение ближайшего месяца погасят долги перед банком?

Решение. Среднее значение КТЛ:

1) 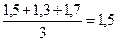2) .

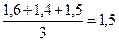Среднее значение КТЛ у обоих должников одинаково, поэтому по лемме Маркова получим одинаковую вероятность погашения долга у обоих должников:

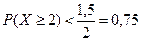, т.е. менее 75%.

Неравенство Чебышев кроме среднего значения КТЛ учитывает еще и его колеблемость (дисперсию), которая у первого больше, чем у второго:

,

.

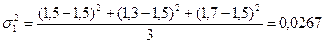Должники погасят долг, если повысят свой КТЛ до уровня 2. Для этого он должен отклониться в большую сторону от существующего значения как минимум на 0,5. Вероятность такого отклонения по неравенству Чебышева равна:

для 1) 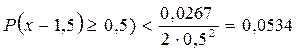, т.е. 5,34%,

для 2) , т.е. 1,34%.

Таким образом, вероятность невозврата долга первым должником будет как минимум 100 – 5,34 = 94,66 %, а вторым – как минимум 100 – 1,34 = 98,66 %.

Почему должник с меньшей колеблемостью показателей вернет ссуду с меньшей вероятностью? меньшая колеблемость КТЛ у второго должника говорит о его большей устойчивости в состоянии неплатежеспособности. Поэтому и вероятность невозврата им долга оказалась выше. Если бы у него была меньшая колеблемость вблизи значения КТЛ, равного, например, 2,5, тогда все обстояло бы по-другому.

Дата добавления: 2014-12-16