И катастрофического рисков на основе неравенства Чебышева

Определение границ зон допустимого, критического

Если в результате некоторого вида предпринимательской деятельности оценена величина m = M(x) и s² = s²(х), а также определены величины критериев к_дп, к_кр, к_кт, то границы зон риска можно оценит следующим образом.

Пусть m = l_ms, х_дп = l_дпs, х_дп > m (случай х_дп < m характеризует ситуацию, неблагоприятную для предпринимательской деятельности, поскольку верхняя граница зоны допустимых убытков меньше величины ожидаемых, т.е. средних, убытков).

Тогда

Отсюда (l_дп - l_m)² к_дп ³ 1; ; .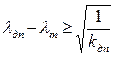

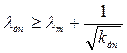Учитывая, что х_дп > m, получаем:

,

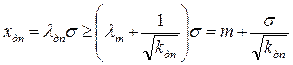т.е. .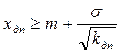

Аналогично,

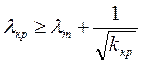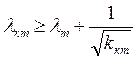Þ ,

Þ .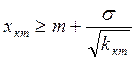

Таким образом, минимальное значение пороговых значений возможных убытков:

, , .

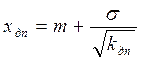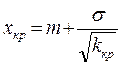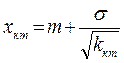Пример 11.

Используем условия примера 3, т.е. считаем, что к_дп = 0,2, к_кр = 0,02, к_кт = 0,002; М(х) = 27,66; s(х) = 26,189 и оценим теоретические границы зон различных относительных убытков.

Решение.

.

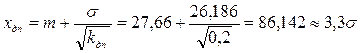
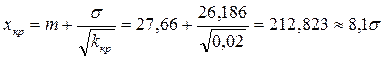
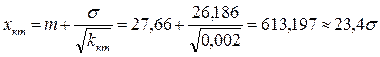Как видим, полученные значения не совпадают с результатами решения примера 3: х* _дп = 39,33, х* _кр = 104,376, х* _кт = 201,14. Это объясняется тем, что здесь при выведении формул для оценок х _дп, х _кр и х _{к т} использовались неравенства (например, для х _дп):

,

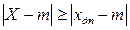которые, в отличие от результата, полученного ранее, учитывают как оценку

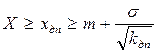, так и оценку ,

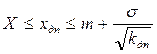т.е. имеет место следующее соотношение:

.

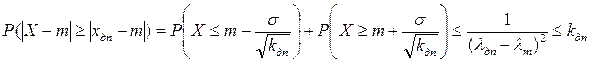Действительно, ранее получили:

.

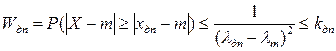Отсюда следует:

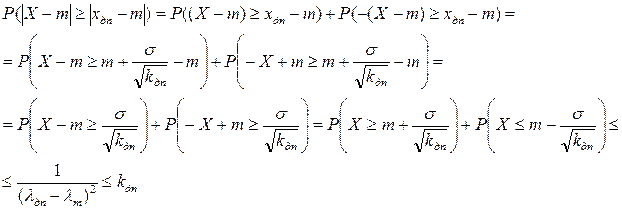
Если же имеются основания считать, что

,

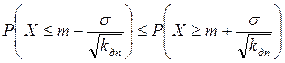(например, если М₀(Х)»М(Х), т.е. функция плотности вероятности распределения является симметричной относительно прямой х = m), то приходим к оценке:

,

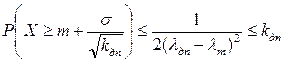т.е. .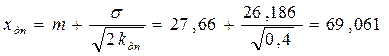

Аналогично получим, что

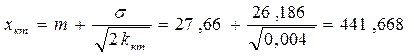
Отличие последних результатов от полученных в примере 3 теперь объясняется тем, что неравенство Чебышева не учитывает свойства функции плотности распределения вероятностей.

2.РИСК В ОТНОСИТЕЛЬНОМ ВЫРАЖЕНИИ

Выбор наименее рискованного решения из нескольких альтернатив на основе сравнения их дисперсии (или полувариации) часто оказывается затруднительным из-за близости величин рассматриваемых показателей. Поэтому сравнению подвергают степени риска в относительном выражении.

В относительном выражении риск определяется как отношение величины убытков к некоторой базе. За базу принимают имущество предпринимателя, общие затраты ресурсов на данный вид деятельности или ожидаемую прибыль.

1. Соотношение максимального объема убытка и объема собственных ресурсов (W):

,

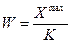где X^max – максимально возможный размер убытков;

К – объем собственных финансовых ресурсов.

С помощью этого коэффициента измеряют риск банкротства. По данным исследований специалистов оптимальный коэффициент риска составляет 0,3, а коэффициент риска, ведущий к банкротству, равен 0,7 и более.

Дата добавления: 2014-12-16