
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Данные для расчета коэффициентов Фехнера
|
|
|
|
| Магазин | Число работников, тыс. чел. | Товарооборот, усл. ден. ед. | Отклонение от средних величин
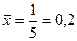 и и 
| Сравнение знаков
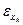 и и 
| ||
| к | 
| 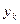
| 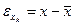
| 
| совпадение
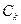
| несовпадение

|
| 0,2 | 3,1 | +0,0 | -0,9 | |||
| 0,1 | 3,1 | -0,1 | -0,9 | |||
| 0,4 | 5,0 | +0,2 | +1,0 | |||
| 0,2 | 4,4 | +0,0 | +0,4 | |||
| 0,1 | 4,4 | -0,1 | +0,4 | |||
| Итого | 1,0 | 20,0 | - | - |
По (1) имеем
 .
.
Направление взаимосвязи в вариациях численности работников и объема товарооборота - положительное (прямолинейное): знаки в отклонениях  и
и 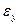 в своем большинстве (в 3 случаях из 5) совпадают между собой. Теснота взаимосвязи переменных по шкале Чеддока - слабая.
в своем большинстве (в 3 случаях из 5) совпадают между собой. Теснота взаимосвязи переменных по шкале Чеддока - слабая.
Коэффициенты парной, чистой (частной) и множественной (совокупной) линейной корреляции Пирсона, в отличие от коэффициента Фехнера, учитывают не только знаки, но и величины отклонений переменных. Для их расчета используют разные методы. Так, согласно методу прямого счета по несгруппированным данным, коэффициент парной корреляции Пирсона имеет вид
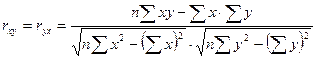 . (2)
. (2)
Этот коэффициент также изменяется от -1 до +1.
При наличии нескольких переменных рассчитывается коэффициент множественной (совокупной) линейной корреляции Пирсона. Для трех переменных х, у, z он имеет вид
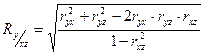 . (3)
. (3)
Этот коэффициент изменяется от 0 до 1.
Если элиминировать (совсем исключить или зафиксировать на постоянном уровне) влияние z на x и у, то их "общая" связь превратится в "чистую", образуя чистый (частный) коэффициент линейной корреляции Пирсона
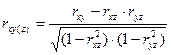 . (4)
. (4)
Этот коэффициент изменяется от -1 до +1. Квадраты коэффициентов корреляции (2) - {4) называются коэффициентами (индексами) детерминации, соответственно, парной, чистой (частной), множественной (совокупной):
 ;
;
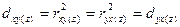 ; (5)
; (5)
 .
.
Каждый из коэффициентов детерминации изменяется от 0 до 1. Он оценивает степень вариационной определенности в линейной взаимосвязи переменных, показывая долю вариации одной переменной у, обусловленную вариацией другой (других) – х и y. Многомерный случай наличия более трех переменных здесь не рассматривается.
Согласно работам английского статистика Р. Э. Фишера (1890 - 1962), статистическая значимость парного и чистого (частного) коэффициентов корреляции Пирсона проверяется в случае нормальности их распределения, на основании t -распределения английского статистика В. С. Госсета (псевдоним "Стьюдент"; 1876 - 1937) с заданным уровнем вероятностной значимости 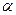 и имеющимися степенями свободы
и имеющимися степенями свободы 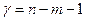 , где m - число связей (факторных переменных). Для парного коэффициента
, где m - число связей (факторных переменных). Для парного коэффициента 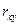 имеем его среднеквадратическую ошибку
имеем его среднеквадратическую ошибку 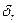 и фактическое значение t -критерия Стьюдента
и фактическое значение t -критерия Стьюдента
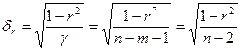 ;
; 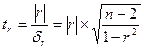 . (6)
. (6)
Для чистого коэффициента корреляции  при расчете его
при расчете его 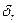 , вместо
, вместо  надо брать
надо брать 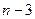 , так как в этом случае т = 2 (две факторные переменные х и z). При большом числе
, так как в этом случае т = 2 (две факторные переменные х и z). При большом числе 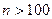 , вместо
, вместо  или
или 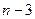 в (6) можно брать п, пренебрегая точностью расчета.
в (6) можно брать п, пренебрегая точностью расчета.
Если  , то коэффициент парной корреляции - общий или чистый является статистически значимым, а при
, то коэффициент парной корреляции - общий или чистый является статистически значимым, а при 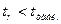 - статистически незначимым.
- статистически незначимым.
Значимость коэффициента множественной корреляции R проверяется по F -критерию Фишера путем расчета его фактического значения
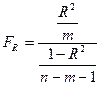 . (7)
. (7)
При  коэффициент R считается статистически значимым с заданным уровнем значимости
коэффициент R считается статистически значимым с заданным уровнем значимости 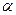 и имеющимися степенями свободы
и имеющимися степенями свободы 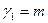 и
и 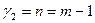 , а при
, а при  - статистически незначимым.
- статистически незначимым.
В совокупностях большого объема 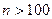 для оценки значимости всех коэффициентов Пирсона вмести критериев t и F применяется непосредственно нормальный закон распределения (табулированная функция Лапласа-Шеппарда).
для оценки значимости всех коэффициентов Пирсона вмести критериев t и F применяется непосредственно нормальный закон распределения (табулированная функция Лапласа-Шеппарда).
Наконец, если коэффициенты Пирсона не подчиняются нормальному закону, то в качестве критерия их значимости используется Z -критерий Фишера, который здесь не рассматривается.
Условный пример расчета (2) - (7) дан в табл. 12.2, где взяты исходные данные табл. 12.1 с добавлением к ним третьей переменной z - размера общей площади магазина (в 100 кв. м).
Таблица 12.2
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 404; Нарушение авторских прав?; Мы поможем в написании вашей работы!