
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ранговая корреляция
|
|
|
|
Коэффициенты линейной корреляции Пирсона имеют своей теоретической предпосылкой нормальное или близкое к нему распределение переменных и их количественное выражение. При других Условиях возникает непараметрическая корреляция, в частности, ранговая корреляция, которая применяется в тех случаях, когда наблюдения неравноценны между собой или когда переменные (признаки) - качественные. Ранги бывают несвязными и связными - соответственно неповторяющимися и повторяющимися по наблюдениям  , задаваясь субъективно или по специальным методикам.
, задаваясь субъективно или по специальным методикам.
Среди всех ранговых показателей важнейшими являются ранговые коэффициенты парной линейной корреляции  и
и 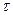 английских статистиков-биометриков Ч. Спирмена (1863 - 1945) и М. Кендэла (род. 1907). В случае неповторяющихся (несвязных) рангов
английских статистиков-биометриков Ч. Спирмена (1863 - 1945) и М. Кендэла (род. 1907). В случае неповторяющихся (несвязных) рангов  и
и  для переменных
для переменных  и
и 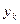 в их наблюдениях
в их наблюдениях  искомые ранговые коэффициенты равны:
искомые ранговые коэффициенты равны:
а) 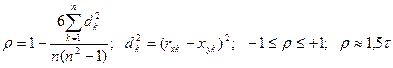 ;
;
б) 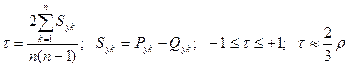 , (8)
, (8)
где: 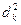 - квадрат разности рангов
- квадрат разности рангов  и
и  двух переменных х и y в наблюдении к;
двух переменных х и y в наблюдении к;
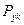 - число рангов
- число рангов 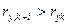 , превышающих данный ранг
, превышающих данный ранг  зависимой переменной у, при сравнении ее наблюдения k со всеми последующими наблюдениями
зависимой переменной у, при сравнении ее наблюдения k со всеми последующими наблюдениями 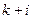 для
для  ;
;
 - аналогичное число последующих рангов, не превышающих данный ранг
- аналогичное число последующих рангов, не превышающих данный ранг  ;
;
 - сумма превышающих и не превышающих рангов.
- сумма превышающих и не превышающих рангов.
Ранги  и
и  для
для  и r обычно задаются целочисленными - от 1 до n и в зависимости от исходных значений переменных
и r обычно задаются целочисленными - от 1 до n и в зависимости от исходных значений переменных  и
и 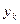 : чем эти значения больше (меньше), тем выше (ниже) их ранги. Например, наименьшие значения х и y получают свои единичные
: чем эти значения больше (меньше), тем выше (ниже) их ранги. Например, наименьшие значения х и y получают свои единичные 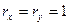 , а наибольшие - свои максимальные ранги
, а наибольшие - свои максимальные ранги 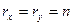 . В принципе возможна другая система ранжирования переменных по их наблюдениям.
. В принципе возможна другая система ранжирования переменных по их наблюдениям.
Для многомерного случая наличия m переменных на основе 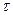 определяется коэффициент линейной конкордации (экспертного согласия) Кендэла - коэффициент множественной ранговой корреляции, который в случае несвязных рангов имеет вид
определяется коэффициент линейной конкордации (экспертного согласия) Кендэла - коэффициент множественной ранговой корреляции, который в случае несвязных рангов имеет вид
 . (9)
. (9)
Случай связных (повторяющихся) рангов для показателей  ,
, 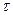 , W здесь не рассматривается ввиду громоздкости математических выражений и трудоемкости расчетов.
, W здесь не рассматривается ввиду громоздкости математических выражений и трудоемкости расчетов.
Значимость коэффициентов Спирмена и Кендэла оценивается по-разному. Значимость  при
при 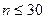 проверяется по "Таблице значимости коэффициентов Спирмена", которая разработана английскими биометриками Г. Т. Глиссером и Р. Ф. Винтером в 1961 г. и приводится в редких русских источниках. Поэтому чаще всего используется классический t -критерий Стьюдента путем расчета его фактического значения
проверяется по "Таблице значимости коэффициентов Спирмена", которая разработана английскими биометриками Г. Т. Глиссером и Р. Ф. Винтером в 1961 г. и приводится в редких русских источниках. Поэтому чаще всего используется классический t -критерий Стьюдента путем расчета его фактического значения 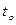 на основе среднеквадратической ошибки
на основе среднеквадратической ошибки 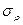
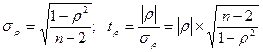 . (10)
. (10)
Если 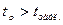 , то коэффициент
, то коэффициент  статистически значим с заданным уровнем значимости
статистически значим с заданным уровнем значимости 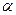 и имеющимися степенями свободы
и имеющимися степенями свободы  , а при
, а при 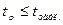 - статистически незначим.
- статистически незначим.
Значимость 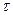 при
при 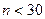 оценивается аналогично (10), с учетом замены
оценивается аналогично (10), с учетом замены  на
на 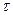 и
и 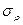 на
на  .
.
При большом числе наблюдений, когда 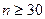 , значимость
, значимость 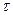 оценивается по нормальному закону, путем расчета на основе ошибки
оценивается по нормальному закону, путем расчета на основе ошибки  его порогового значения
его порогового значения 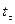 :
:
 ; (11)
; (11)
где 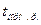 - аргумент нормального закона (табулированной функции Лапласа-Шеппарда) при заданном уровне доверительной вероятности
- аргумент нормального закона (табулированной функции Лапласа-Шеппарда) при заданном уровне доверительной вероятности  .
.
Если  , то коэффициент
, то коэффициент 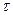 статистически значим, а при
статистически значим, а при  - статистически незначим. Значимость W проверяется по
- статистически незначим. Значимость W проверяется по  - распределению Пирсона путем расчета его фактического значения
- распределению Пирсона путем расчета его фактического значения
 . (12)
. (12)
При 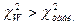 коэффициент W значим с уровнем значимости
коэффициент W значим с уровнем значимости 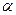 и числом степеней свободы
и числом степеней свободы 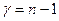 , а при
, а при  - незначим.
- незначим.
Все критерии (10) - (12) рассмотрены для случая несвязных рангов. Практически считается, что  ,
, 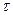 , W являются значимыми, когда они превышают число 0,5. В табл. 12.3 - 12.5 на условных данных проведен расчет коэффициентов для несвязных рангов с единым уровнем значимости
, W являются значимыми, когда они превышают число 0,5. В табл. 12.3 - 12.5 на условных данных проведен расчет коэффициентов для несвязных рангов с единым уровнем значимости 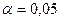 .
.
Таблица 12.3.
Подготовка данных для расчета рангового коэффициента  Спирмена
Спирмена
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 489; Нарушение авторских прав?; Мы поможем в написании вашей работы!