Регрессионный анализ для ортогональных двухуровневых планов

Благодаря выбору ортогонального плана и равномерному дублированию опытов (два параллельных опыта в каждой из восьми комбинаций уровней факторов) вычислительная процедура для нашего примера оказывается очень простой и сводится к следующей схеме.

1. Оценка дисперсий среднего арифметического в каждой строке плана эксперимента

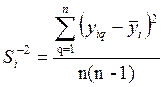
где y_iq — результат отдельного опыта, — среднее значение отклика по повторным опытам, п — количество параллельных опытов, q — номер параллельного опыта, q=1….n, i — номер строки матрицы плана, i = 1... N.

2. Проверка однородности дисперсий с помощью критерия Кохрена G.

Критерий Кохрена определяется отношением максимальной дисперсии к сумме всех дисперсий:

С этим критерием связаны числа степеней свободы п- 1 и N. Гипотеза об однородности дисперсий не отвергается, если экспериментальное значение критерия Кохрена не превысит табличного.

3. Если дисперсии однородны, то рассчитывается оценка
усредненной дисперсии воспроизводимости:

В реальных условиях гипотеза об однородности дисперсий подтверждается далеко не всегда. Тогда можно идти различными путями. Например, найти преобразование зависимой переменной, отыскать иной закон распределения случайной величины или обратиться к какому-нибудь робастному статистическому методу. Этот этап относится к выбору модели ситуации.

4. Мы уже говорили о том, что благодаря ортогональности плана вычислительная процедура сильно упрощается:

,

где x_ji — значение j-го фактора в i-ом опыте, и,j - номера факторов, j, u=0,1,..., k, .

5. Проверка гипотезы об адекватности модели основана
на расчетах дисперсии адекватности 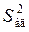и критерия Фишера (F-критерия)

, ,

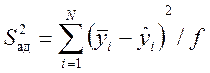где 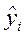— рассчитанное по уравнению регрессии значение отклика, f — число степеней свободы, связанное с дисперсией адекватности, р — число оцениваемых коэффициентов регрессии. Рассчитанное значение F-критерия сравнивается с табличным значением, определяемым числами степеней свободы f и N (п—1). Если экспериментальная величина F-критерия не превышает табличного значения, гипотеза об адекватности модели не отвергается.

'6. Проведем проверку значимости коэффициентов регрессии. Поскольку план ортогонален, они определяются с одной и той-же дисперсией:

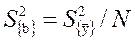
Далее для коэффициентов регрессии рассчитывается доверительный интервал

с некоторой доверительной вероятностью. В этом выражении t-критерий (критерий Стьюдента) имеет то же число степеней свободы, что и дисперсия воспроизводимости

Коэффициент значим, если его абсолютная величина больше доверительного интервала.

7, Незначимые коэффициенты регрессии исключаются,
и вновь проводится проверка адекватности модели со значимыми коэффициентами.

8. Статистический анализ завершается интерпретацией модели в терминах объекта исследования.

Продолжение примера. А теперь приведем численные результаты. В. табл. 4 даны значения дисперсий среднего арифметического для каждой строки плана эксперимента. Критерий Кохрена G=0,302/0,853=0,35. Ниже помещен фрагмент таблицы критерия Кохрена для уровня значимости 0,05:

n-1 N
	0,727	0,561	0,480
	0,679	0,515	0,437
	0,638	0,477	0,402

Табличное значение для п —1 = 1 и N=8 равно 0,679. Экспериментальная величина G-критерия меньше этого значения, в силу чего гипотеза об однородности дисперсий не отвергается*. Это позволяет рассчитать усредненную оценку дисперсии воспроизводимости . Число степеней свободы равно N(n-1)=8(2-1)=8

* Наш пример носит главным образом иллюстративный характер. На практике же делать выводы при наличии одной степени свободы рискованно.

Таблица 5 Расчетная таблица и результаты опытов

Номер опыта	Аддитивная постоянная	Матрица планирования	Векторы - столбцы взаимодействия	Экспериментальный отклик
X0	X1	X2	X3	X1X2	X1X2	X1X2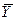
	+ 1	- 1	-1	-1	+1	+1	+1	3,75
	+ 1	- 1	+1	+1	-1	-1	+1	2,75
	+ 1	- 1	+1	-1	-1	+1	-1	-0,50
	+ 1	- 1	-1	+1	+1	-1	-1	2,25
	+ 1	+ 1	- 1	-1	-1	-1	+1	2,75
	+ 1	+ 1	-1	+1	-1	+1	-1	0,75
	+ 1	+ 1	+1	-1	+1	-1	-1	- 1,00
	+ 1	+ 1	+1	+1	+1	+1	+1 -	0,50

Для получениякоэффициентоврегрессии составляется расчетная таблица (табл. 5).

Коэффициенты регрессии равны:

b0 = 1,406,		b2 = -0,968,		B3 = 0,156,
b12 = -0,031,		b13 = -0,281,		B23 = 1,031.

Информация, требуемая для проверки гипотезы адекват­ности, приведена в табл. 6. Например, для первого опыта 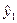=1,406-0,656 (-1)-0,968 (-1) +0,156 (-1) -0,031 * (-1) -0,281 (-1) (-1) +1,031 (-1) (-1) =3,593. Число степеней свободы дисперсии адекватности f=8—7=1 и сама дисперсия равна .

Критерий Фищера для проверки гипотезы адекватности модели F==0,195/0,107= 1,82. Приведем фрагмент таблицы F-критерия для уровня значимости 0,05.

f N(n-1)
	5,6	4,7	4,4
	5,3	4,5	4,1
	5,1	4,3	3,9

Расчет дисперсии адекватности

Номер опыта					Номер опыта
	3,750	3,593	0,157	246,49		2,750	2,905	-0,155	240,25
	2,750	2,593	0,157	246,49		0,750	0,593	0,157	246,49
	-0,500	-0,343	-0,157	246,49		-1,000	-1,155	0,155	240,25
	2,250	2,405	-0,155	240,25		0,500	0,657	-0,157	246,49

Расчет дисперсии адекватности для модели со значимыми
коэффициентами регрессии

Номер опыта					Номер опыта
	3,750	3,780	-0,030			2,750	3,030	-0,280
	2,750	2,406	0,344			0,750	0,406	0,344
	-0,500	-0,218	-0,282			-1,000	-0,968	-0,032
	2,250	2,280	-0,030			0,500	0,532	-0,032

В нашем случае f=8—7=1, N (п —1)=8, табличное значение F-критерия равно 5,3. Экспериментальная величина F-критерия не превышает табличного значения, поэтому гипотеза об адекватности выбранной модели не отвергается.

Число степеней свободы	t-критерий
	2,57
	-2,45
	2,37
	2,31

Далее найдем значимые коэффициенты регрессии. Дисперсия коэффициентов регрессии

Из фрагмента таблицы для t-критерия (уровень значимости 0,05) следует, что в нашем случае t=2,31. Доверительный интервал

Оставляя только значимые коэффициенты регрессии,

получим 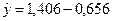x₂ — 0,968 х₂— 0,281 x₂х₃+1,031 x₂х₃. Предсказанные значения зависимой переменной и данные для расчета дисперсии адекватности приведены в табл. 7.

В этом случае

f=8-5=3;

;

Табличное значение F-критерия при f=3, N (n-1)=8 равно 4,1 и гипотеза об адекватности модели не отвергается. Займемся теперь интерпретацией модели,

Как интерпретировать?

Задача интерпретации весьма сложна. Ее решают в несколько этапов.

Первый этап состоит в следующем. Устанавливается, в какой мере каждый, из факторов влияет на параметр оптимизации. Величина коэффициента регрессии — количественная мера этого влияния. Чем больше коэффициент, тем сильнее влияет фактор. О характере влияния факторов говорят знаки коэффициентов. Линейные коэффициенты полинома являются частными производными функции отклика по соответствующим переменным. Их геометрический смысл — тангенсы углов наклона гиперплоскости к соответствующей оси. Больший по абсолютной величине коэффициент соответствует большему углу наклона и, следовательно, более существенному изменению параметра оптимизации при изменении данного фактора.

Продолжение примера. Вернемся к нашему примеру. Сразу видно, что априорные соображения экспериментатора в значительной степени подтвердились, поскольку значимыми оказались не только линейные эффекты факторов, но и некоторые парные взаимодействия. Из трех линейных эффектов выделились два: эффект фактора х₁ — концентрации сахарина и фактора х₂ —плотности тока,

Судя по количественной, оценке коэффициентов, плотность тока влияет несколько сильнее концентрации сахарина. Характер их влияния одинаков. С увеличением концентрации и плотности тока внутренние напряжения уменьшаются, так как коэффициенты регрессии имеют отрицательный знак. Температура (x₃) в выбранных интервалах варьированная не оказывает значимого влияния на внутреннее напряжение, поскольку линейный коэффициент b₃ незначим. Но влияние этого фактора проявилось весьма сильным образом в парных взаимодействиях. Ведь эффект совместного влияния плотности тока и температуры (b₂₃) превосходит по величине даже линейные эффекты. Смысл эффекта взаимодействия состоит в том, что влияние одного фактора зависит от того, на каком уровне находится другой фактор.

К росту отклика будет вести одновременное увеличение х₂ и х₃ или их одновременное уменьшение. Задача же экспериментатора состоит в уменьшении отклика. Поэтому надо либо уменьшать х₃ и увеличивать х₃, либо наоборот. Коэффициент взаимодействия b ₁₃ имеет отрицательный знак. Это означает, что уменьшение внутреннего напряжения связано с действием концентрации сахарина и температуры в одном направлении: либо надо одновременно увеличивать концентрацию и температуру, либо уменьшать. Этот эффект взаимодействия по величине заметно уступает всем остальным значимым эффектам.

Воспользуемся полученным ранее уравнением для отыскания оптимальных условий осаждения. Особый интерес представлял поиск условий проведения процесса при концентрации сахарина 0.6 1,06 г/л (x₁=-0,33 1,2), плотности тока 60 80 А/дм² (x₂=0,2 l,0), температуре 50 60 °C (x₃=0,33 1,0). При этом получались качественные покрытия заданного состава. В практических целях достаточно иметь уравнения для температур 50, 55 и 60 °С, что было сделано подстановкой в уравнение регрессии кодированных значений х₃ (0,33; 0,66 и 1,0). Принимая у=0, получим

0,749 x₁+0,625 x₂=1,406;

0,841 x₁+0,286 х₂= 1,406;

0,937 x₁-0,063 х₂=1;406.

Из последних двух уравнений следует, что даже при х₂ = 1, х₁>1,3, т. е. концентрация сахарина выходит за заданный интервал. Поэтому для определения значений факторов, обеспечивающих минимальные внутренние напряжения, необходимо пользоваться только первым уравнением. Полагая x₂=1,0, согласно уравнению получим x₁=1,04. Натуральные значения факторов: концентрация сахарина 1,01 г/л, плотность тока 80 А/дм², температура электролита 50 °С. Несколько опытов, проведенных в данных условиях, подтвердили, что внутренние напряжения покрытий действительно близки к нулю.

Дата добавления: 2014-11-29