Основное преимущество факторного эксперимента

Основное преимущество факторного эксперимента заключается в том, что в эксперименте варьируются одновременно все факторы. Это приводит к тому, что дисперсия в оценке коэффициентов регрессии оказывается в N раз меньше ошибки опыта.

При классическом подходе эксперименты ставятся в определенной последовательности: все факторы фиксируются на некотором уровне, а один фактор переводят на другой уровень. Затем это повторяют для другого фактора. В оценке каждого из коэффициентов уравнения участвует только какая-то часть опытов.

Рассмотрим пример двух факторов и классический подход в экспериментировании.

Результаты эксперимента представлены в табл. 3.

Таблица 3. Неоптимальная схема эксперимента для двух факторов

опыты	x0	x1	x2	y
	+1	+1	+1	y1
	+1	+1	-1	y2
	+1	-1	+1	y3

Каждый коэффициент уравнения опре­деляют по двум точкам:

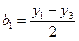
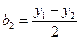
с дисперсией где 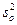— ошибка опыта.

При использовании факторного эксперимента следует поставить четыре опыта, т. е. реализовать ПФЭ 2². Коэффициенты уравнения определяют по результатам четырех опытов и дисперсия будет равна:

.

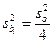Точность проведения эксперимента в этом случае вдвое выше. Для достижения такой точности при классическом подходе необходимо 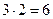опытов. Еще более показательна эта особенность факторного эксперимента при большом количестве факторов. Так, при числе факторов n = 7 воспользуемся частью (1/16) ПФЭ 2⁷, поставив всего 8 опытов, как и при классическом подходе. Однако дисперсия в оценке коэффициентов уравнения в этом случае будет

против той же, что и ранее 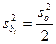. Для такой же

высокой точности при классическом подходе следует поставить 8 х 4 = 32 опыта.

Достоинства ПФЭ:

1.независимость дисперсии переменной состояния от вращения системы координат в центре плана;

2.одинаковая и минимальная дисперсия коэффициентов регрессии;

3.независимость определения коэффициентов регрессии друг от друга;

4.простота в вычислениях коэффициентов.

Последние два свойства ПФЭ можно оценить на конкретном примере, используя понятия матричной алгебры (см. приложение 2).

Рассмотрим план типа ПФЭ 2² (см. табл.1), для которого X – матрица факторов и Y – столбец наблюдений имеет вид:

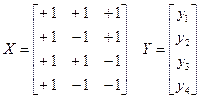
Найдем произведение матриц:

Система нормальных выражений записывается:

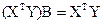(10)

(11)

Решение системы в общем виде

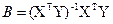(12)

Или для конкретного примера:

(13)

Из выражения (13) видно, что свободный член уравнения регрессии
b₀ равен среднему арифметическому всех значений выходной переменной
(х₀ = 1), а b₁ и b2, находят как среднее алгебраической суммы y_u со знаками столбца х₁ или х₂. Простота расчета коэффициентов уравнения регрессии не вызывает сомнения. Ясно также, что вычеркивание или добавление столбцов x_i не меняет расчет дру­гих коэффициентов, т. е. коэффициенты регрессии определяются независимо друг от друга.

Дата добавления: 2014-11-29