
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проверка адекватности линейного уравнения регрессии
|
|
|
|
Принятие решений
Если для какого-то коэффициента условия (78) и (80) не выполняются, то соответствующий фактор можно признать незначимым и исключить его из уравнения регрессии.
Однако надо быть осторожным и всегда помнить, что в предварительном эксперименте уже отсеивались незначимые факторы, скорее всего полученная незначимость фактора является следствием неудачно выбранного интервала варьирования: он был выбран малым. Более правильным является решение повторить эксперимент при расширенном интервале варьирования для исследуемого фактора. Конечно, при этом число опытов, а значит, время эксперимента, возрастает. Иногда половину опытов сохраняют тем, что расширение интервала варьирования проводят только в одну сторону: один (верхний или нижний) уровень остается.
Если фактор остался незначимым после повторения эксперимента и всех необходимых расчетов, то его (или их) отбрасывают и переходят к оценке адекватности полученной математической модели.
Пригодность линейного уравнения регрессии для решения задачи поиска области оптимума проверяется методом, изложенным в гл. II, § 6. Сравниваются две дисперсии — одна показывает рассеяние средних опытных данных переменной состояния  относительно тех значений переменной состояния
относительно тех значений переменной состояния  , которые предсказаны полученным линейным уравнением регрессии. Эта дисперсия называется дисперсией адекватности и рассчитывается по формуле:
, которые предсказаны полученным линейным уравнением регрессии. Эта дисперсия называется дисперсией адекватности и рассчитывается по формуле:
 (26)
(26)
где m — число параллельных опытов; N — число строк матрицы планирования; l — число членов в уравнении регрессии, оставшихся после оценки значимости.
Вторая дисперсия — это ошибка опыта. Адекватность проверяют, оценивая отношение
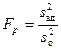 (27)
(27)
по критерию Фишера
 (28)
(28)
для степеней свободы fад = N — l, f0 = N (m — 1) и заданного уровня значимости q. Если выполняется условие (28), то линейное уравнение регрессии признается адекватным, т. е. рассеяние экспериментальных данных переменной состояния относительно уравнения регрессии того же порядка, что и рассеяние, вызванное случайными изменениями в объекте исследования (ошибка опыта).
Таблица 7. Формула расчета ПФЭ2n
| Блоки | Формулы расчета | Обозначения |
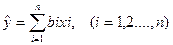 Или
Или

|  – переменная состояния расчетная); – переменная состояния расчетная);
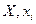 – факторы; – факторы;
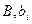 – коэффициенты уравнения регрессии; – коэффициенты уравнения регрессии;
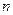 – число факторов; – число факторов;
 – переменная состояния (экспериментальная); – переменная состояния (экспериментальная);
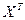 – транспонированная матрица X; – транспонированная матрица X;
 – число опытов – число опытов
 – построчная дисперсия; – построчная дисперсия;
 –переменная состояния (в параллельных опытах) –переменная состояния (в параллельных опытах)
 – расчетные значения критерия Кохрена; – расчетные значения критерия Кохрена;
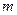 – число параллельных опытов – число параллельных опытов
 – табличное значение критерия Кохрена; – табличное значение критерия Кохрена;
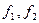 – число степеней свободы; – число степеней свободы;
 – уровень значимости – уровень значимости
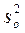 – ошибка опыта (дисперсия воспроизводимости); – ошибка опыта (дисперсия воспроизводимости);
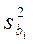 – дисперсии коэффициентов; – дисперсии коэффициентов;
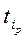 – расчетное значение критерия Стьюдента; – расчетное значение критерия Стьюдента;
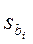 – среднеквадратичные отклонения – среднеквадратичные отклонения
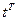 – табличное значение критерия Стьюдента; – табличное значение критерия Стьюдента;
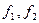 – число степеней свободы; – число степеней свободы;
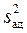 – дисперсия адекватности; – дисперсия адекватности;
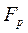 – расчетное значение критерия Фишера – расчетное значение критерия Фишера
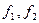 – число степеней свободы – число степеней свободы
| |
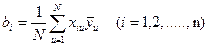
| ||
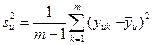

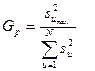
| ||
| 3а | Условие однородности
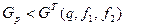


| |


| ||

| ||
| 5а | Условие значимости коэффициентов
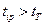

| |

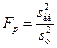
| ||
| 6а | Условие адекватности модели
 (q, f1,f2) (q, f1,f2)

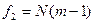
|

Рис. 4. Алгоритм расчета и анализа математической модели
При расчете Fp предполагается, что  >
>  . Однако на практике бывает, что
. Однако на практике бывает, что 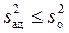 . Тогда вывод об адекватности модели может быть сделан без проверки условия (23).
. Тогда вывод об адекватности модели может быть сделан без проверки условия (23).
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 729; Нарушение авторских прав?; Мы поможем в написании вашей работы!