Построение матрицы планирования

План, содержащий запись всех комбинаций факторов или их части в кодированной форме, называется матрицей планирования. Таблица 1, например, является матрицей планирования для двух факторов на двух уровнях.

Для построения матрицы планирования с большим числом факторов можно использовать следующий прием.

Элементарное сочетание первого фактора (+1, -1) повторяется для каждого следующего фактора на верхнем и нижнем уровнях. Этот прием распространяется на построение матриц любой размерности. Столбец х₀ — это столбец значений фиктивной переменной.

Этот прием построения матриц планирования можно трактовать как прием чередования знаков. Действительно, в первом столбце знаки не меняются, во втором — меняются поочередно, в третьем — они чередуются через два, в четвертом — через 4 и т. д. (по показателям степеней двойки).

Свойства матрицы планирования. Рассмотренные матрицы планирования обладают такими свойствами, которые позволяют считать, что их построение выполнялось оптимально с точки зрения получаемой но результатам реализации матрицы планирования математической модели. Если мы ищем модель в виде уравнения регрессии, то коэффициенты должны быть наилучшими и точность предсказания значений переменной состояния одинакова в любом направлении факторного пространства. Эти требования формули­руются как условия ортогональности и р ототабельности.

Таблица 2
№п/п	Тип эксперимента	Факторы
x0	x1	x2	x3	x4	x5
	ПФЭ 2^5	ПФЭ 2^4	ПФЭ 2^3	ПФЭ 2^2	+1	+1	+1	+1	+1	+1
	+1	-1	+1	+1	+1	+1
	+1	+1	-1	+1	+1	+1
	+1	-1	-1	+1	+1	+1
		+1	+1	+1	-1	+1	+1
		+1	-1	+1	-1	+1	+1
		+1	+1	-1	-1	+1	+1
		+1	-1	-1	-1	+1	+1
			+1	+1	+1	+1	-1	+1
			+1	-1	+1	+1	-1	+1
			+1	+1	-1	+1	-1	+1
			+1	-1	-1	+1	-1	+1
			+1	+1	+1	-1	-1	+1
			+1	-1	+1	-1	-1	+1
			+1	+1	-1	-1	-1	+1
			+1	-1	-1	-1	-1	+1
				+1	+1	+1	+1	+1	-1
				+1	-1	+1	+1	+1	-1
				+1	+1	-1	+1	+1	-1
				+1	-1	-1	+1	+1	-1
				+1	+1	+1	-1	+1	-1
				+1	-1	+1	-1	+1	-1
				+1	+1	-1	-1	+1	-1
				+1	-1	-1	-1	+1	-1
				+1	+1	+1	+1	-1	-1
				+1	-1	+1	+1	-1	-1
				+1	+1	-1	+1	-1	-1
				+1	-1	-1	+1	-1	-1
				+1	+1	+1	-1	-1	-1
				+1	-1	+1	-1	-1	-1
				+1	+1	-1	-1	-1	-1
				+1	-1	-1	-1	-1	-1

Симметричность относительного центра эксперимента - алгебраическая сумма элементов в вектор-столбце для каждого фактора равна 0

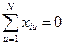(4)

Условие нормировки – сумма квадратов элементов каждого столбца равна числу опытов.

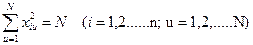(5)

где n — число факторов; N — число опытов (или строк матрицы планирования).

Условие ортогональности предполагает равенство нулю суммы почленных произведении любых двух столбцов матрицы:

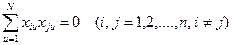(6)

Эти условия легко проверить по табл. 2. Действительно, полный факторный эксперимент типа 2" является ортогональным.

Ортогональные планы ПФЭ (для линейных моделей) имеют также еще одно свойство — рототабельность.

Рототабельность - предполагает равенство и минимальность дисперсии предсказанных значений переменной состояния для всех точек факторного пространства.

По закону накопления ошибок можно записать для дисперсии предсказанных уравнением регрессии значений переменной состояния:

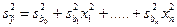(7)

где 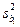— дисперсия коэффициентов модели b_i.

Из условия (6) вытекает, что дисперсии коэффициентов регрессии равны между собой. Тогда можно записать:

(8)

Учитывая, что 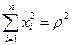где радиус сферы:

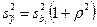(9)

Отсюда ясно, что дисперсия предсказанного значения выходной переменной зависит только от радиуса сферы. Это свойство рототабельностн эквивалентно независимости дисперсии выходной переменной от вращения координат в центре плана и оправдано при поиске оптимума градиентными методами..

Дата добавления: 2014-11-29