Приклад 5. 9

Завод виробляє два види пилососів: "Равлик " (Р) і "Коник " (К) (табл. 5.21).

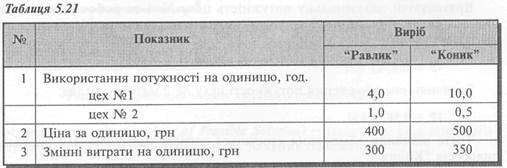
Виробничий процес здійснюється у двох цехах: складальному (№ 1) і випробу­вальному (№ 2), які мають потужність 1 000 і 150 годин відповідно.

Запаси матеріалів для виробництва пилососів "Коник " дають змогу виробля­ти лише 90 пилососів щодня.

Необхідно визначити, скільки пилососів кожного виду слід виготовляти щодня для максимізації прибутку.

Побудова моделі

Побудова моделі лінійного програмування передбачає: / визначення змінних величин; / визначення цільової функції та побудову її рівняння; / визначення обмежень та побудову їх рівнянь.

У моделі лінійного програмування комбінації продукції кількість кожного її виробу і є змінною величиною.

Цільова функція (Objective Function) — мета, якої намагається досягти менеджер.

Рівняння цільової функції (Objective Function Equation) — алгебраїчне зображен­ня мети, якої намагається досягти менеджер у процесі лінійного програмування.

У нашому прикладі метою є максимізація прибутку або маржинального до­ходу через оптимальну комбінацію виробів.

Отже, оптимальною комбінацією виробів є така комбінація, що дає компанії змогу досягти мети, зображеної рівнянням цільової функції.

Оскільки цільовою функцією розглядуваної компанії є максимізація загаль­ного маржинального доходу, визначимо його величину на одиницю кожного виробу.

Маржинальний дохід на одиницю продукції, грн:

Пилосос Р: 400 - 300 = 100 Пилосос К: 500 - 350 = 150

Виходячи з цього, рівняння цільової функції матиме вигляд: Загальний маржинальний дохід = 100 Р + 150 К

У нашому прикладі існує три основні обмеження: потужність цеху № 1, по­тужність цеху № 2 та матеріальні запаси для виробництва.

Рівняння обмеження (Constraint Equation) — алгебраїчне зображення одного з обмежувальних чинників.

Враховуючи максимальну потужність цеху № 1 та робочий час, необхід­ний для складання одиниці продукції, складемо рівняння обмеження потуж­ності цеху № 1:

4Р + 10К<1 000 За рівнянням обмеження потужності цеху № 2 матиме вигляд:

1Р + 0,5К< 150

Третє рівняння обмеження стосується запасів матеріалів для виробництва пилососів "Коник":

К< 90.

Нарешті, ще одне обмеження лінійного програмування передбачає неможли­вість негативного виробництва, тобто:

Р>0, К>0.

Вирішення моделі лінійного програмування

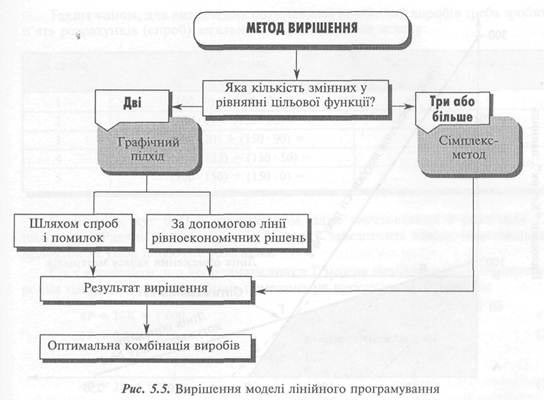
На практиці моделі лінійного програмування розв'язують переважно за допомогою комп'юте­ра. При цьому, залежно від кількості змінних у рівнянні цільової функції (рис. 5.5) можна засто­совувати різні методи вирішення.

У нашому прикладі ми маємо справу з двома виробами, тому вирішен­ня моделі лінійного програмування можна здійснити шляхом графічного підходу.

Графічний підхід до вирішення моделі лінійного програмування означає по­будову графіка, в якому вісі координат відображають значення змінних величин, і вже за графіком — визначення зони можливих рішень.

Зона можливих рішень (Area of Feasible Solution) — площа графіка лінійного програмування, окреслена лініями рівнянь наявних обмежень.

Для окреслення зони можливих рішень насамперед необхідно визначити ко­ординати ліній обмежень.

Для цього розрахуємо максимальний щоденний обсяг виробництва:

Виходячи з цього, можемо записати координати ліній обмежень:

Наведені координати дають змогу побудувати графік і визначити зону мож­ливих рішень (рис. 5.6).

Як бачимо, зоною можливих рішень є площа АБВГД.

Оптимальна комбінація виробів (Optimal Product Mix) — це завжди кут зони можливих рішень!

Отже, який з п'яти кутів наведеної зони можливих рішень є оптимальним? Відповідь на це запитання можна отримати шляхом спроб і помилок або за допо­могою лінії рівноекономічної величини.

Розв'язання шляхом спроб і помилок передбачає послідовне підставляння координат кожного кута зони можливих рішень у рівняння цільової функції.

Спроба, яка покаже найбільше значення показника цільової функції, озна­чатиме оптимальну комбінацію виробів.

Кути наведеної зони можливих рішень мають такі координати:

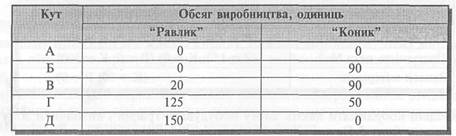
Таким чином, для визначення оптимальної комбінації виробів треба зробити п'ять розрахунків (спроб) загального маржинального доходу:

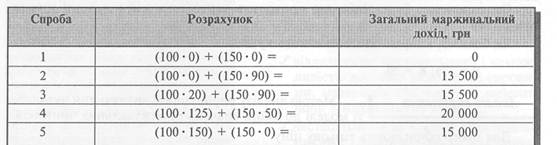
Як бачимо, кут ВГД є оптимальним, адже виготовлення й реалізація 125 пилососів "Равлик" і 50 пилососів "Коник" забезпечить заводу максимальний прибуток за умов існуючих обмежень.

Слід відзначити, що координати точки Г можна визначити шляхом перетво­рення наведених раніше рівнянь обмежень на просту систему рівнянь:

4Р + 10К= Г000 (1)

1Р + 0,5К=150 (2)

Помножимо друге рівняння на 4:

4Р + 2К = 600 (3)

Віднімемо рівняння (3) з рівняння (1) і знайдемо значення К:

8К = 400

К = 50. Введемо значення К в рівняння (2) і знайдемо значення Р:

IP + 0,5 (50) = 150 Р = 150 - 25 = 125

Альтернативний шлях знаходження оптимального кута передбачає викорис­тання лінії рівноекономічних рішень.

Для цього на графіку проводять лінію цільової функції, яка перетинає зону можливих рішень побудови і використання лінії рівноекономічних рішень.

Припустімо, що загальний маржинальний дохід дорівнює 6000. У цьому разі рівняння цільової функції матиме вигляд:

100Р + 150К = 6 000,

а можливі координати точок на графіку будуть: Р = 0; К = 40 Р = 60; К = 0.

Лінія, проведена через ці точки на графіку, буде первинною лінією рівноеко-номічної величини. Вона зображена на рис. 5.2 пунктиром.

Наступний крок — проведення ліній, паралельних первинній лінії рівноеко-номічної величини. і

Оптимальною буде лінія, що проходить через останній кут зони можли­вих рішень.

Як бачимо, координати останнього кута: Р = 125; К = 50.

Аналіз вирішення

Метою аналізу вирішення є визначення чутливос­ті ті моделі до зміни значень обмежувальних чинників.

Для цього обчислюють тіньову ціну.

Тіньова ціна (Shadow Price) — величина зниження значення цільової функції внаслідок зменшення значення відповідного обмежувального чинника на одну одиницю.

Розглянемо розрахунок тіньової ціни на прикладі цеху № 1. Припустімо, що потужність цього цеху зменшилася на одну годину.

У цьому разі система рівнянь обмежень матиме вигляд:

4Р + 10К = 999

1Р + 0,5К= 150

Виникає питання: на скільки зменшиться маржинальний дохід компанії у цьому разі? Щоб відповісти на це питання, необхідно розв'язати наведену систе­му рівнянь. Для цього помножимо друге рівняння на 4 і знайдемо значення К:

4Р + 10К = 999

4Р + 2К = 600

8К = 399 Отже, К = 49,88. Тепер підставимо значення К у рівняння та знайдемо Р:

IP + 0,5 (49,88) = 150 Р = 150 - 24,94 Р = 125,06.

З урахуванням нових значень К і Р визначимо загальний маржинальний дохід:

(100 • 125,06) + (150 • 49,88) = 12 506 + 7 482 = 19 988.

Таким чином, у разі зменшення потужності цеху № 1 на одну годину загальний маржинальний дохід компанії відповідно зменшиться на 12 грн (20 000 - 19 988).

5.4. РІШЕННЯ СТОСОВНО ЗАПАСІВ

Виробничі й торгівельні підприємства зазвичай інвестують значні кошти відповід­но у виробничі й товарні запаси. Це зумов­лено різними причинами, зокрема:

/ віддаленістю постачальника і немож­ливістю доставки необхідних сирови­ни, матеріалів або товару в момент, коли у них виникне потреба;

/ нестабільними зв'язками з постачаль­никами і невпевненістю, що поста­чальник забезпечить необхідною си­ровиною чи матеріалами відповідної якості в потрібний момент;

/ очікуваним підвищенням цін на си­ровину, матеріали або товари;

• ризиком нестачі ресурсів у разі рап­тового зростання попиту тощо.

У зв'язку з цим система планування й контроль придбання, виробництва та реалі­зації запасів значною мірою визначають ус­піх підприємства, особливо за умов неста­більної економіки та жорсткої конкуренції.

Виходячи з цього, основною метою

управління запасами є своєчасні поставки запасів і мінімізація витрат, пов'яза­них із замовленням і зберіганням їх.

Одним з найпоширеніших методів управління запасами є метод економічно­го розміру замовлення.

Економічний розмір замовлення (Economic Order Quantity — EOQ) — це кіль­кість замовлених запасів, що забезпечує оптимальну комбінацію витрат на при­дбання та зберігання їх.

Для визначення оптимального рівня замовлення запасів треба враховувати релевантні витрати на придбання та зберігання їх.

Релевантними є лише ті витрати, що змі­нюватимуться залежно від рівня запасів. Ви­трати, на які не будуть впливати зміни рів­ня запасів, не є релевантними.

Витрати, пов'язані з запасами, включають:

/ витрати на закупку;

/ витрати на замовлення;

/ витрати на зберігання;

/ можливі втрати внаслідок браку запасів.

Витрати на закупку (Purchase Costs) за­пасів, як правило не є релевантними, бо ви­трати на придбання одиниці запасу не змі-

нюються, за винятком випадків, коли при закупівлі великої кількості матеріалів або товарів покупцеві надаються знижки.

Витрати на замовлення (Ordering Costs) запасів охоплюють витрати на оформ­лення документів і здійснення розрахунків, пов'язаних із замовленням.

Витрати на виконання замовлення, однакові для всіх варіантів створення запасів, не є релевантними, тому при визначенні оптимального розміру замов­лення враховуються тільки додаткові витрати на розміщення замовлення.

Релевантними витратами на замовлення запасів, виготовлених самим під­приємством, звичайно є витрати на переналагодження обладнання для випуску відповідної партії виробів.

До витрат на зберігання (Holding or Carrying Costs) належать витрати, пов'я­зані зі зберіганням матеріалів, готової продукції або товарів на складі. Частина витрат на зберігання запасів є релевантною. Наприклад, заробітна плата комір­ника, амортизація обладнання й постійна орендна плата за обладнання і примі­щення не належать до релевантних витрат, оскільки на них не впливає зміна обсягу запасів.

Релевантні витрати на зберігання запасів зазвичай включають:

/додаткові витрати на страхування запасів;

/ додаткові витрати на утримання складських приміщень;

/ додаткові витрати на обробку матеріалів;

/ втрати внаслідок знецінення запасів;

/ можливу втрату прибутковості інвестицій.

Можливі втрати прибутковості інвестицій — це альтернативні витрати, по­в'язані з інвестуванням коштів у запаси. Ці витрати відображають прибуток, втра­чений через інвестування коштів у запаси, а не використання їх в інших напря­мах. До альтернативних витрат належать лише ті, що змінюються залежно від кількості куплених одиниць запасів. Релевантні витрати на обробку матеріалів, витрати внаслідок морального зносу та погіршення характеристик запасів врахо­вувати дуже важко. Тому такі витрати часто виражають у відсотках до прямих витрат на зберігання одиниці запасів.

Втрати через нестачу запасів (Inventory Shortage Costs) — можливі втрати че­рез відсутність достатньої кількості запасів для задоволення виробничих потреб або потреб клієнтів.

Такі втрати містять:

/ втрачений дохід від продажу;

/ штрафні санкції за несвоєчасну поставку продукції замовникам;

/ понаднормативні витрати внаслідок заміни матеріалів дорожчими;

/ втрати внаслідок простоїв тощо.

Втрати через нестачу запасів не враховують при визначенні економічного розміру замовлення, але беруть до уваги при обчисленні моменту розміщення замовлення.

Отже, оптимальний розмір замовлення визначається тими витратами, на які справляє вплив або кількість запасів, що зберігаються, або кількість зроблених замовлень. Чим більша кількість одиниць замовляється одночасно, тим менше замовлень необхідно зробити за рік, тобто зменшуються витрати на виконання

замовлень. Однак коли робиться менше замовлень, необхідно мати більший се­редній задас, що веде до збільшення витрат на зберігання запасів. Проблема полягає в тому, щоб знизити витрати на зберігання великих запасів порівняно з витратами на розміщення великої кількості замовлень. Оптимальним розміром замовлення буде така замовлена кількість, за якої загальні витрати на замовлення і зберігання запасів будуть мінімальними. Оптимальний економічний розмір за­мовлення можна визначити:

/табличним методом;

/графічним методом;

/за допомогою формули.

Для ілюстрації цих методів розглянемо такий приклад.

Дата добавления: 2014-11-29