Метод планов

Пользуясь данным методом для конкретного мгновенного значения времени, можно построить планы положений, скоростей и ускорений точек звеньев механизма.

Планом положения механизма называют выполненное в масштабе (μ_ℓ) графическое изображение взаимного расположения звеньев, соответствующее выбранному моменту времени.

Построение плана положений механизма начинают с изображения его кинематической схемы при заданном положении ведущего звена. Положение ведомых звеньев механизма определяют методом геометрических засечек, фиксируя положение кинематических пар. Обычно планы механизма строят для 12 или 24 положений ведущего звена. Траекторию любой точки механизма легко определить из этих планов, соединяя одноименные точки плавной кривой. Величины и направления скоростей и ускорений точек механизма наглядно представляются планами скоростей и ускорений. Построение планов скоростей и ускорений основано на графическом решении векторных уравнений распределения скоростей и ускорений в твердом теле.

Рис. 2.1

При плоском движении точки звеньев механизма перемещаются в плоскостях, параллельных некоторой неподвижной плоскости. Рассмотрим плоское движение твердого тела (рис. 2.1). Его положение будем определять по положению отрезка АВ, соединяющего две точки тела. Положения I и II тела определяются положением отрезков А₁В₁ и А₂В₂. Отрезок А₁В₁ можно привести в положение А₂В₂ путем поступательного движения с кинематическими параметрами точки (полюса) А (отрезок займет положение А₂В'₁) и вращательного движения отрезка на угол Δφ₁ вокруг полюса А₂. Аналогично возможно перемещение отрезка А₁В₁ в положение А₂В₂ путем поступательного движения с параметрами точки В и вращения отрезка вокруг точки В₂ на угол Δφ₂. Угол поворота отрезка (тела) не зависит от выбора полюса (Δφ₁ = Δφ₂). Плоское движение тела слагается из поступательного (переносного) с кинематическими параметрами выбранной точки (полюса) тела и вращательного (относительного) движения вокруг этой точки. Обычно за полюс принимают точку с известными параметрами движения. Скорость (ускорение) любой точки тела, совершающего плоское движение, равна сумме скорости (ускорения) полюса в поступательном (переносном) движении и скорости (ускорения) во вращательном (относительном) движении вокруг полюса.

Рассмотрим два характерных случая.

1. Две точки А и В (рис. 2.2, а) принадлежат одному звену и удалены друг от друга на расстояние . Скорость и ускорение точки А известны, ее примем за полюс, тогда , где – скорость точки В во вращательном движении вокруг точки А ().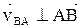

Изобразим в масштабе μ_v ((м/с)/мм) скорости точек А и В отрезками p_v a и p_vb, отложенными из произвольно выбранной точки p_v (рис. 2.2, б), p_v a = v_A/μ_v; p_vb = v_B/μ_v, соединим концы этих отрезков (точки а и b). Полученный треугольник p_v a b называется планом скоростей звена, а точка p_v – полюсом плана скоростей.

Угловую скорость звена ω можно определить по формуле ω = v_BA/ℓ = = (a b×μ_v) / . Направление ω определится, если вектор 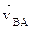приложить в точке В. Обычно направление относительных скоростей определяют из плана скоростей – относительная скорость направлена к той букве плана скоростей, которая стоит первой в индексе при 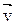, например, вектор 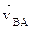направлен от а к b, вектор от b к а.

Ускорения точек А и В объединены уравнением

.

Полное относительное ускорение во вращательном движении точки В вокруг точки А состоит из нормального , направленного к центру вращения точки В, т.е. от В к А, и тангенциального , направленного перпендикулярно отрезку АВ. Модуль нормального ускорения определяем, используя план скоростей = = 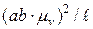. Тангенциальное ускорение определяется по формуле = ε .

План ускорений звена АВ в масштабе μ _a [(м/с²)/мм] изображен на рис. 2.2, г. Ускорения точек А и В изображены отрезками p _aa ' и p _a b', отложенными из общей точки p _a – полюса плана ускорений. Отрезок a 'n в масштабе представляет ускорение , а отрезок nb' – ускорение . Тогда ε = (nb'×μ _a) / , а направление ε определится, если приложить вектор в точку В (вектор из плана ускорений).

2. Две точки А₁ и А₂ принадлежат двум звеньям 1 и 2, образующим поступательную пару, и совпадают в рассматриваемый момент времени (рис. 2.3, а). Скорость и ускорение точки А₁ известны. Скорость точки А₂ равна 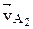= , где – скорость точки А звена 1, совпадающей с точкой А звена 2 (переносная скорость точки А₂); – скорость звена 2 относительно звена 1, направленная параллельно звену 1. План скоростей для рассматриваемого случая представлен на рис. 2.3, б.

Ускорение точки А₂, когда переносное движение не поступательное (рис. 2.3, в), складывается из трех ускорений: переносного (т.е. ускорения точки А₁), поворотного (кориолисова) и относительного

.

Величина поворотного ускорения равна = , где ω₁ – угловая скорость звена 1. Направление кориолисова ускорения покажет вектор скорости ; если его повернуть на 90° в сторону вращения кулисы 1, т.е. в направлении ω₁.

Вектор ускорения 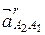звена 2 относительно звена 1 направлен вдоль звена I. План ускорений для рассматриваемого случая показан на рис. 2.3, г.

Как видно из планов скоростей и ускорений, их полюсы (p_v, p _a) изображают точки, абсолютные скорости и ускорения которых равны нулю.

Рассмотрим применение метода планов для кулисного механизма. Схема механизма показана на рис. 2.4, а. Звено 1 является ведущим и вращается равномерно с угловой скоростью ω₁. В масштабе μ_ℓ вычерчиваем схему механизма для заданного положения кривошипа 1. Так как длина О₂A зависит от положения кривошипа 1, определяем ее из схемы механизма. Строим план скоростей. Скорость центра шарнира (точки А_{1, 2}) и направлена перпендикулярно звену 1 в сторону ω₁. Изобразим эту скорость в масштабе μ_v в виде отрезка p_v a ₁ = .

а

б

в

а

г

б

в

г

а

б

в

Рис. 2.3

Рис. 2.2

	Рис. 2.4

Определим скорость 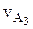той точки А кулисы 3, которая в данный момент совпадает с центром шарнира А. Рассматривая движение точки А₃ сначала по отношению к центру шарнира А, а затем по отношению к точке O₂, запишем соответственно два векторных уравнения:

;

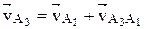. (2.11)

Скорость скольжения 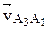точки А₃ кулисы 3 относительно центра А₁ шарнира направлена параллельно О₂A₁; – относительная скорость точки А₃ во вращательном движении звена 3 вокруг точки О₂. Эта скорость направлена перпендикулярно звену 3. Точка О₂ неподвижна, т.е. = 0. Уравнения (2.11) решаем графически (рис. 2.4, б): проведем из точки а ₁ прямую, параллельную АО₂, а из полюса p_v – прямую, перпендикулярную О₂A. Точка пересечения их определит положение конца вектора абсолютной скорости точки А₃ кулисы 3 – точку а ₃. Вектор 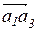покажет направление относительной скорости 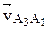. Из плана скоростей имеем

| .

Направление ω₃ укажет вектор 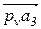, если его приложить в точке А₃ кулисы 3. В данном положении кулиса 3 вращается против часовой стрелки.

Перейдем к построению плана ускорений (рис. 2.4, в). Ускорение центра шарнира А равно = (, т.к. ε = 0). Вектор 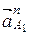направлен от точки А к точке О₁. На плане это ускорение изобразим отрезком . Определим ускорение точки А₃ кулисы 3, совпадающей в данном положении механизма с центром шарнира А₁. Рассматривая движение точки А₃ кулисы 3 сначала по отношению к центру шарнира А₁, а затем по отношению к центру вращения кулисы О₂, запишем два векторных уравнения:

;

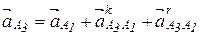. (2.12)

Ускорение известно, а 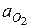= 0. Кориолисово ускорение определим по формуле

.

Оно направлено в ту же сторону, в которую окажется направлен вектор , если его повернуть на 90° в направлении угловой скорости ω₃ кулисы 3. Вектор относительного ускорения точки А₃ (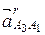) кулисы по отношению к ползуну 2 направлен параллельно O₂А. Вектор нормального ускорения точки А₃, возникающего при вращении кулисы 3 вокруг точки O₂, направлен от точки А к центру O₂. Величина этого ускорения равна

.

Вектор тангенциального ускорения точки A₃ кулисы в ее вращательном движении вокруг точки O₂ направлен перпендикулярно звену 3. Решаем уравнения (2.12) графически. Из точки 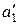отложим отрезок 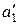k, который в масштабе μ _a изображает , и через точку k проведем прямую, параллельную O₂А. Из полюса р _a (так как = 0) отложим отрезок р _a n₃ в масштабе μ _a, изображающий , и через точку n₃ проведем прямую, параллельную . На пересечении прямых, параллельных и 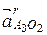, получим точку – конец вектора ,т.е. абсолютного ускорения точки А₃.

Векторы и 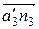изображают в масштабе μ _a соответственно ускорения 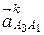и . Величина углового ускорения кулисы определяется из плана ускорений

.

Направление ε₃ определится вектором , если его перенести в точку A₃ кулисы. В данном случае направление ε₃ противоположно направлению ω₃, т.е. кулиса вращается замедленно.

Дата добавления: 2014-11-29