Метод кинематических диаграмм

Определение перемещений (S, φ), скоростей (v, ω) и ускорений (a, ε) рассмотренными выше методами ведется для ряда положений механизма, близко отстоящих друг от друга. Обычно период движения ведущего звена механизма разбивают на 12 положений и для каждого из них строят план механизма. По полученным значениям этих величин могут быть построены графики, носящие название кинематических диаграмм. Каждая кинематическая диаграмма обычно представляет собой графическое изображение изменения одного из кинематических параметров звеньев или точек звеньев исследуемого механизма в функции времени или перемещения ведущего звена. Например, для кривошипно-ползунного механизма (см. рис. 1.7) можно построить кинематические диаграммы перемещений S_c, скоростей v_c и ускорений a _c точки С ползуна в зависимости от угла поворота φ кривошипа: S_c = S_c(φ); v_c = v_c(φ); a _c = a _c(φ) или времени t: S_c = S_c(t) и т.д.

Наиболее просто строить кинематические диаграммы перемещений звеньев (точек) механизма. Для их построения достаточно наличие только планов положений звеньев механизма. Пусть на рис. 2.5, а задана кинематическая диаграмма пути S = S(φ); S = S(t). Определение скоростей и ускорений основано на методе графического дифференцирования.

Графическое дифференцирование. Для построения диаграммы скоростей воспользуемся зависимостью

v = . (2.13)

Скорость точки в рассматриваемый момент времени пропорциональна тангенсу угла наклона касательной в соответствующих точках кривой диаграммы перемещений. Формула (2.13) является основой графического дифференцирования: определение истинных скоростей сводится к проведению касательных к кривой S = S(t) и определению тангенсов углов наклона их к оси абсцисс. Вместо касательных проще проводить хорды, что приводит к более простому, но менее точному методу – методу хорд, когда кривую S = S(t) заменяют вписанной в нее ломаной линией. Сущность метода хорд заключается в следующем. Делим отрезок оси абсцисс 0–5 (см. рис. 2.5, а) на равное число частей 0–1; 1–2 и т.д. и в точках 1, 2, 3, 4, 5 проводим ординаты до пересечения с кривой S = S(t) в точках 1', 2', …, 5'. Соединив эти точки прямыми, получаем ломаную линию 0'–1'–2'–…–5'. Для построения диаграммы скорости выбираем начало новой системы координат – точку О₁ (рис. 2.5, б). На оси абсцисс откладываем влево от точки О₁ произвольный отрезок О₁P₁ = H₁, называемый полюсным расстоянием. Затем через точку Р₁ проводим лучи Р₁1₁; Р₁2₁ и т.д., параллельные хордам 0–1¢; 1¢–2¢; …; 4¢–5¢, отсекающие на оси ординат отрезки, пропорциональные средним скоростям на участках 0–1;
1–2; …; 4–5 и удовлетворяющие соотношениям:

О₁1₁ = H₁tgα₁ = H₁ ,

где 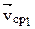– масштабная средняя скорость на отрезке времени Dt₁ (см. рис. 2.5, а).

Отрезок О₁1₁ изображает среднюю скорость в масштабе μ_v = , т.е. 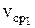= |О₁1₁|×μ_v.Для получения кривой v_cp = v_cp(t) необходимо полученные ординаты О₁1₁; О₁2₁; …; О₁5₁ масштабных значений средних скоростей перенести на середины соответствующих отрезков (Δt / 2) оси абсцисс и вершины ординат, т.е. точки 1₁', 2₁', …, 5₁' соединить плавной кривой. Истинное значение средней скорости в каждый момент определяется по формуле

v = μ_v× 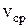. (2.14)

Дифференцируя графическим путем кривую v = v (t), можно получить кинематическую диаграмму ускорений a = a (t). Методика построения кривой a = a (t) ничем не отличается от построения v = v (t). Чем меньше участки, на которые разбиваем исследуемую кривую вдоль оси абсцисс, тем точнее метод дифференцирования.

Рассмотренный метод широко применяется для кинематического исследования механизмов. Анализ кинематических диаграмм v = v (t) и a = a (t) (особенно последний) позволяет судить о величине динамических нагрузок, возникающих в механизме, а следовательно, надежности механизма. Избежать ударов в механизмах можно лишь тогда, когда ускорение звеньев на кинематической диаграмме a = a (t) изменяется плавно. Поэтому часто задаются (например, для кулачковых механизмов) графиком ускорений толкателя, а искомый график его перемещений находят методом графического интегрирования. Так поступают и в том случае, если нас не интересует закон движения толкателя, а устанавливается только его максимальный ход (h). Например, такие требования предъявляются к кулачковым механизмам, применяемым в различных реле, в командных устройствах.

Графическое интегрирование. Пусть задана диаграмма v = v (t) (рис. 2.6, а). Тогда путь исследуемой точки за некоторый промежуток времени определится как S = μ_v μ_t . Отсюда видно, то задача построения интегральной кривой S = S(t) по заданной v = v (t) сводится к определению и суммированию площадей ряда вертикальных полос. Эту задачу можно выполнить графически следующим образом. Разделим кривую v = v (t) точками a, b, c, d, e на участки, соответствующие моментам времени 0–1; …; 4–5. Величины отрезков, определяющих средние скорости на каждом участке точками 1₀, 2₀ и т.д. снесем на ось ординат в точки 1₁, 2₁, …, 5₁. Эти точки лучами соединим с полюсом Р, выбранном на оси абсцисс на расстоянии Н от точки О. Затем, выбрав начало (точку О₁) новой системы координат (рис. 2.6, б), в пределах соответствующих делений 0₁–1; 1–2; …; 4–5 по оси абсцисс последовательно проводим линии 0₁ а ₁; a ₁b₁; b₁c₁; … параллельные лучам Р1₁; Р2₁ и т.д. Через полученные точки (a ₁; b₁; c₁; …) проведем плавную кривую, являющуюся диаграммой пути S = S(t). Масштаб диаграммы пути равен μ_s = μ_vμ_tH(м/мм).

Рассмотренный выше метод графического интегрирования широко применяется при синтезе кулачковых механизмов. Под синтезом понимают определение формы и размеров кулачка, удовлетворяющих тем движениям, которые должен осуществлять толкатель.

б

б

а

а

Рис. 2.5 Рис. 2.6

Дата добавления: 2014-11-29