Силы трения

Трением называют сопротивление относительному движению соприкасающихся тел, возникающее в местах их контакта. Силы трения чаще всего производят отрицательную работу, так как они всегда направлены в сторону, противоположную скорости относительного движения звеньев в кинематических парах.

Виды трения. В зависимости от характера относительного движения соприкасающихся звеньев различают трение скольжения и трение качения. При трении скольжении одни и те же точки одного тела последовательно приходят в соприкосновение с различными точками другого тела.

Тела могут соприкасаться по поверхности, линии или в точке. Разновидностью трения скольжения является трение верчения, при котором точки контакта тел при их относительном движении описывают концентрические окружности вокруг общей нормали, проходящей через какую-то точку соприкасающихся поверхностей.

При трении качения (рис. 3.5) следующие одна за другой точки одного тела приходят в соприкосновение с различными точками другого тела. При этом дуговые перемещения точек контакта по поверхностям соприкосновения обоих тел одинаковы по величине и знаку (АВ = АВ'). При трении качения относительная скорость соприкасающихся тел в точке контакта равна нулю. Сопротивление перекатыванию зависит от упругих свойств материалов соприкасающихся тел, диаметра тел качения, величины прижимающей силы, состояния поверхностей соприкосновения (смазка, загрязнения), скорости и других факторов. Из-за деформации в месте контакта (рис. 3.5) равнодействующая сила нормальных давлений N смещена на некоторое расстояние в сторону движения и равна прижимающей силе G. Величину k называют коэффициентом трения качения, она определяется экспериментально и имеет размерность длины. При равномерном перекатывании цилиндра под действием силы F, приложенной в центре цилиндра, в месте контакта возникает сила сопротивления относительному движению F_k, равная по величине движущей силе F. При равномерном движении имеют место не только равенства сил N = G, F_k = F, но и моментов сил N·k = F·r. Трение качения может сопровождаться трением скольжения.

М_дв

Рис. 3.5 Рис. 3.6

В зависимости от состояния соприкасающихся поверхностей различают несколько видов трения при скольжении: чистое трение, возникающее на поверхностях, освобожденных от адсорбированных пленок или химических соединений; сухое трение, возникающее при воздействии внешней среды и отсутствии смазки и загрязнений между поверхностями; жидкостное трение, при котором поверхности полностью разделены слоем смазки. Кроме того, иногда встречаются еще промежуточные виды трения: полусухое и полужидкостное, при котором наиболее выступающие шероховатости не разделяются слоем смазки и приходят в непосредственное соприкосновение.

При жидкостном трении сцепление жидкости с трущимися поверхностями должно быть больше сцепления слоев жидкости между собой. Силами трения здесь являются силы сопротивления сдвигу отдельных слоев смазки. Возникновение сил наиболее распространенного в практике сухого трения скольжения объясняется наличием шероховатостей соприкасающихся поверхностей и силами молекулярного взаимодействия.

Определение сил трения в кинематических парах. Отношение сил трения к нормальной силе N, сжимающей соприкасающиеся тела, называют коэффициентом трения скольжения f. Величина его определяется экспериментально и зависит от свойств материала соприкасающихся тел, качества поверхности, скорости скольжения, температуры. Различают коэффициент трения покоя f₀, и трения движения f. Первый всегда больше при прочих равных условиях из-за большего влияния сил молекулярного взаимодействия. В инженерных расчетах при определении сил трения скольжения пользуются формулой Амонтона – Кулона

F_тр = f·N. (3.7)

Формулой (3.7) пользуются при определении сил трения в поступательных парах, считая значение коэффициента f трения постоянным. Сопротивление движению во вращательной паре определяет момент сил трения М_тр относительно ее оси. Величина момента равна

М_тр = F_тр · r = N · r · f_вр , (3.8)

где r – радиус соприкасающихся поверхностей пары; N – полное давление (реакция связи) в паре; f_вр – коэффициент трения во вращательной паре, определяемый экспериментально.

При сухом трении для неприработавшихся пар f_вр = (3/2) f, а для приработавшихся пар – f_вр = (4/3) f, где f – коэффициент трения плоских соприкасающихся поверхностей из того же материала.

Явление, при котором относительное движение соприкасающихся звеньев вследствие трения считается невозможным, называется самоторможением.

В высших кинематических парах возможно трение качения, скольжения и качения со скольжением. Момент сил трения качения определяется по формуле

M_k = N · k или M_k = F_k · r, (3.9)

где N – давление в паре; k – коэффициент трения качения; F_k – сила сопротивления; r – радиус кривизны соприкасающегося звена.

Тогда

F_k = 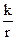N = f_k · N, (3.10)

где f_k – условный (приведенный) коэффициент трения качения.

Сравнивая f_k и f, можно определить вид движения в высшей кинематической паре. Если f > f_k, что имеет место для большинства материалов, происходит только качение; если f < f_k – чистое скольжение и при f_k = f – перекатывание со скольжением.

Трение в фрикционных передачах и передачах с гибкими звеньями. В фрикционных передачах силы трения являются движущими. Рассмотрим фрикционную передачу с круглыми колесами (рис. 3.6). Передача движения от катка 1 к катку 2 осуществляется силой трения F_тр между ними, создаваемой прижатием одного катка к другому некоторой силой N. К катку 1 приложен движущий момент М_дв, а к колесу 2 – момент сопротивления M_c. Передача движения станет возможной, если сила трения F_тр будет достаточной для преодоления окружной силы F_c = 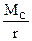, т.е. F_тр > F_c или М_тр > М_c.

В механизмах систем широкое применение нашли передачи с гибкими звеньями в виде лент, ремней, нитей. Как и во фрикционных механизмах, передача движения становится возможной при определенной силе трения между шкивом и гибким звеном. Сила трения между шкивом и лентой возникает в результате натяжения ее концов или ветвей и зависит от ряда факторов, в первую очередь, от величины натяжения концов, дуги охвата и коэффициента трения ленты при движении относительно шкива.

Следует различать случаи, когда лента движется относительно шкива и когда относительное скольжение во всех точках дуги охвата отсутствует.

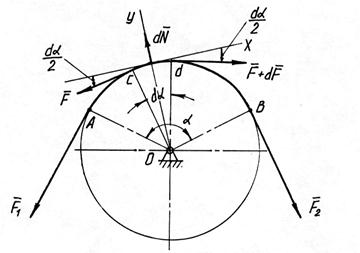
Рис. 3.7

Пусть гибкое звено охватывает круглый шкив (рис. 3.7). Ветвь гибкого звена, которая при движении набегает на шкив, назовем набегающей ветвью, а ветвь, которая сбегает со шкива, – сбегающей ветвью. Дуга, по которой гибкое звено соприкасается со шкивом, называют дугой охвата, а соответствующий ей центральный угол – углом охвата. Натяжение набегающей ветви обозначим F₁, а сбегающей – F₂. Принимаем следующие допущения: гибкое звено считаем нерастяжимым и не оказывающим сопротивления изгибу. При равномерном движении ленты необходимо, чтобы F₂ = F₁ + F_тр, где F_тр – сила трения ленты. Отсюда F_тр = F₂ – F₁, то есть сила, которая действует на шкив. Если сила F_тр больше силы окружного сопротивления на ведомом шкиву, то гибкое звено заставит шкив вращаться. Если же сила окружного сопротивления больше силы трения, гибкое звено будет скользить по шкиву, не приводя его во вращение. Для определения силы трения рассмотрим равновесие элемента нити длиной d = rdα, где r – радиус шкива. Разность натяжений нити в точках c и d, равная dF, уравновешивается силой dF_тр = f dN, где dN – нормальная составляющая силы реакции. Следовательно,

dF = f dN. (3.11)

Величину dN найдем из уравнения равновесия сил, действующих на элемент cd в проекции на ось OY (рис. 3.7). Учитывая, что синус малого угла равен самому углу и пренебрегая величинами высшего порядка, имеем dN = F sin + (F + dF) sin = F dα.

Подставляя значение dN в равенство (3.11), получим

dF = f F dα. (3.12)

Разделим переменные в уравнении (3.12) и, просуммировав их по углу охвата, будем иметь

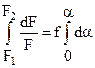или .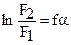

Отсюда следует, что или F₂ = F₁ e^fα. Тогда сила трения

F_тр = F₂ – F₁ = F₁ (e^fα – 1). (3.13)

Из формулы (3.13) видно, что с увеличением силы натяжения ветви F_1, угла охвата a и коэффициента трения скольжения f сила трения растет.

Силы трения вызывают не только энергетические потери, но и оказывают отрицательное влияние на точность кинематических параметров механизмов.

Дата добавления: 2014-11-29