Вывод уравнений Лагранжа второго рода

Уравнение движения механизма

До сих пор предполагалось, что закон движения ведущего звена известен и скорость его постоянна. В действительности кинематические параметры механизмов являются функцией внешних сил, действующих на звенья механизма и масс подвижных звеньев.

Для определения действительного закона движения ведущего звена механизма нужно составить уравнение движения механизма и решить его относительно искомого кинематического параметра.

Наиболее простым и удобным методом определения уравнений движения механизмов является решение лагранжевых уравнений движения в обобщенных координатах.

Перемещения звеньев механизма ограничены имеющимися связями, т.е. не все координаты точек звеньев независимы. Для механизмов положение точек звеньев при известных их размерах определяется заданием только независимых, обобщенных координат.

Обобщенными координатами называют независимые величины любой размерности (м, рад, …), с помощью которых можно выразить положение любой точки механической системы (механизма). Их количество равно числу степени подвижности W механизма или степени его свободы. Будем обозначать обобщенные координаты q₁, q₂, …, q_w. С течением времени звенья механизмов меняют свое положение, поэтому обобщенные координаты, определяющие их положение, зависят от времени q = q(t). Обобщенные скорости и ускорения определяются как , .

Например, для кривошипно-ползунного механизма (см. рис. 1.7), имеющего степень подвижности W = 1, за обобщенную координату принимаем перемещение ведущего звена. При ведущем звене – кривошипе 1 за обобщенную координату выбирают угол его поворота, т.е. q = φ₁, а обобщенные скорости и ускорения будут соответственно равны ; 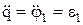. Если же этот механизм служит для преобразования возвратно-поступательного движения во вращательное, т.е. ведущим звеном будет ползун 3, то за обобщенную координату принимают перемещение ползуна q = x_c = S₃, а обобщенные скорости и ускорения будут соответственно равны и .

Наибольшее распространение имеют механизмы со степенью подвижности, равной единице. Рассмотрим вывод уравнения Лагранжа для таких механизмов. Механизм (механическую систему) можно представить как совокупность материальных точек (k = 1, 2, …, n), каждая из которых имеет массу m_k, и на каждую из которых действует некоторая сила . Координаты этих точек выразим через обобщенные координаты . Линейные скорости точек механизма равны

. (3.20)

Из выражения (3.20) имеем

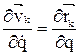. (3.21)

На основании второго закона Ньютона известно дифференциальное уравнение движения точки. Уравнение движения механизма представим как совокупность уравнений движения всех его материальных точек

(k = 1, 2, …, n). (3.22)

Естественно, зависимости (3.22) непригодны для исследования механизмов. Умножим левую и правую части выражения (3.22) скалярно на 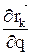и сложим полученные таким образом для всех точек механической системы уравнения. Имеем:

. (3.23)

Введем понятие обобщенной силы – Q. Обобщенную силу определяют из выражения элементарной работы δW всех сил на возможном (бесконечно малом, допускаемом связями) перемещении системы или механизма:

, (3.24)

где – приращение радиуса-вектора точки приложения силы , a δq – приращение обобщенной координаты. Но , следовательно, обобщенная сила равна

. (3.25)

Размерность обобщенной силы зависит от размерности обобщенных координат

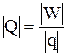. (3.26)

Преобразуем левую часть уравнения (3.23), воспользовавшись равенством (3.21):

Так как сумма представляет собой кинетическую энергию системы (механизма), уравнения движения системы (3.22) запишем в виде одного уравнения в обобщенных координатах следующим образом:

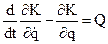. (3.27)

Для механизмов, степень подвижности которых больше единицы, количество уравнений (3.27), как и число обобщенных сил, равно числу обобщенных координат.

Дата добавления: 2014-11-29