О соотношении скоростей в высшей кинематической паре

В месте контакта ведомые и ведущие звенья кулачковых, фрикционных, зубчатых передач образуют высшую кинематическую пару. В этой паре (рис. 2.7) должны выполняться следующие условия:

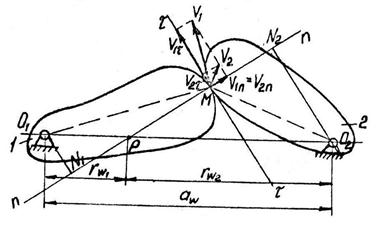
Рис. 2.7

Геометрическое условие. В точке контакта профилей поверхности имеют общую нормаль. Если нормали к поверхностям в точке контакта не будут составлять одну прямую, то профили пересекутся.

Кинематическое условие. Проекции на общую нормаль скоростей контактирующих точек, принадлежащих звеньям 1, 2, одинаковы, т. е. v_1n = v_2n, при невыполнении этого условия контактирующие поверхности разойдутся или внедрятся друг в друга.

Рассмотрим передачу, состоящую из двух звеньев 1 и 2, вращающихся вокруг неподвижных параллельных осей (см. рис. 2.7) с межосевым расстоянием а _w. Точка Р пересечения общей нормали n – n к соприкасающимся поверхностям, которая проведена в точке контакта звеньев с линией, соединяющей их центры вращения О₁О₂, называется полюсом передачи. Расстояния от центров вращения звеньев до полюса называются начальными радиусами(r_w). Линейная скорость звена 1 в точке контакта v₁ = ω₁·O₁M; звена 2 – v₂ = = ω₂·O₂M. Проекции скоросте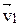й и 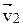на общие нормаль и касательную в точке контакта обозначим v_1n, v_2n и v_1τ, v_2τ. Убедимся, что треугольник, образованный векторами скоростей v_1n,v_1τ и v₁, подобен треугольнику O₁N₁M, а треугольник скоростей v_2n, v_2τ, v₂ – треугольнику O₂N₂M. Из подобия рассмотренных треугольников

.

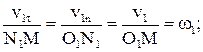
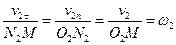Но согласно кинематическому условию v_1n = v_2n или ω₁·O₁N₁ = ω₂·O₂N₂, поэтому ω₁/ω₂ = O₂N₂/O₁N₁.На основании подобия треугольников O₁N₁P и O₂N₂P имеем О₂N₂/O₁N₁ = N₂P/N₁P = O₂P/O₁P. Тогда ω₁/ω₂ = N₂P/N₁P или

ω₁/ω₂ = 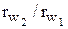. (2.15)

Отношение угловых скоростей (передаточное отношение) звеньев высшей кинематической пары обратно пропорционально начальным радиусам, и при неизменном положении полюса оно постоянно.

Скорость относительного скольжения звеньев в точке их касания равна геометрической разности проекций скоростей на общую касательную

v_ck = v_1τ – v_2τ = ω₁×N₁M – ω₂ ×N₂M =

= ω₁(N₁P + PM) – ω₂(N₂P – PM) = PM(ω₁ + ω₂).

Как видно, при совмещении точки зацепления с полюсом передачи (РМ = 0) скольжение профилей отсутствует и имеет место только их перекатывание.

Из рассмотренного следует, что передача движения в высшей кинематической паре может происходить двояко: а) за счет перекатывания звеньев друг по другу без скольжения, когда движение передается за счет сил трения, возникающих в зоне контакта этих звеньев при надавливании их друг на друга (например, фрикционные передачи); б) за счет взаимного давления звеньев, очерченных по определенным профилям (кулачковые, зубчатые механизмы). В этом случае между касающимися профилями происходит не только перекатывание, но и относительное скольжение. В действительности и первый вид движения сопровождается проскальзыванием.

Кинематика механизмов с высшими кинематическими парами, в частности фрикционных, рассмотрена в подразд. 13.2, зубчатых – в подразд. 14.7.

Глава 3. ДИНАМИКА МЕХАНИЗМОВ

Дата добавления: 2014-11-29