Кинематическая погрешность многоступенчатой передачи

Точность многоступенчатых передач определяется ошибкой положения ведомого звена, зависящей от первичных погрешностей изготовления (погрешность шага, эксцентриситет и т.д.) и сборки (погрешность межосевого расстояния, перекосы осей, погрешность из-за зазоров в опорах т.п.), а также силовых и температурных деформаций деталей.

Так как число возможных причин, вызывающих ошибку положения ведомого звена зубчатой передачи, велико и определение их влияния часто затруднительно, точность нереверсивных передач оценивают практически по комплексному показателю – наибольшей кинематической погрешности F_ir', которая при расчетах оценивается по допускаемым отклонениям F_i'.

Исходными параметрами для расчета ошибки ведомого звена являются: модуль m, число зубьев всех зубчатых колес передачи z, степень точности передачи. Модуль и число зубьев определяют из кинематического расчета механизма.

Величину допускаемой кинематической погрешности для всех зубчатых колес определяем, пользуясь зависимостью (14.14) и данными табл. 14.1 и 14.2, она задается в микрометрах по делительной окружности. Выразим кинематическую погрешность колеса в угловых минутах, так как эта размерность лучше характеризует погрешность угла поворота

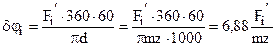, уг. мин, (14.15)

где d – диаметр делительной окружности; m – модуль в мм; z – число зубьев колеса.

Рассмотрим вначале одноступенчатую зубчатую пару 1, 2. Суммарная ошибка положения (перемещения) δφ_i∑ ведомого звена 2 будет равна

δφ_i∑ = δφ_i(1-2) + δφ_i2, (14.16)

где δφ_i(1-2) – величина кинематической погрешности второго звена, вызванная погрешностью звена 1; δφ_i2 – величина собственной кинематической погрешности колеса 2.

Так как передаточное отношение i₁₂ = ω₁/ω₂ = δφ_i1/δφ_i(1-2), поэтому погрешность δφ_i1 ведущего колеса 1 вызовет погрешность поворота колеса 2, равную

δφ_i(1-2) = δφ_i1/i₁₂, (14.17)

где δφ_i1 – величина собственной кинематической погрешности колеса 1. Тогда выражение (14.16) представим как

δφ_i∑ = δφ_i1/i₁₂ + δφ_i2,

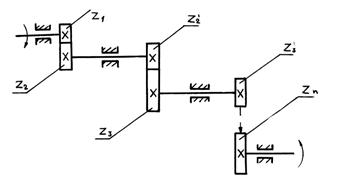
Максимальная кинематическая погрешность многоступенчатого механизма (рис. 14.15) равна сумме приведенных к ведомому звену n кинематических погрешностей всех колес передачи

δφ_i∑ = δφ_i1/i_1n + δφ_i2/i_2n + … + δφ_in = 6,88 [ 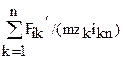]. (14.18)

Здесь δφ_i∑ – величина максимальной кинематической погрешности многоступенчатого механизма в угловых минутах, т.е. максимальной ошибки положения (перемещения) ведомого звена n; z_k – число зубьев колеса с номером k; F_ik' – допускаемые отклонения (шага, профиля зубьев) k-го звена в мкм; i_kn – передаточное отношение от k-го колеса к звену n; m – модуль зубчатой передачи в миллиметрах.

Рис. 14.15  

Дата добавления: 2014-11-29