Проверочный и проектировочный расчеты прямозубой цилиндрической передачи на сопротивление усталости при изгибе

г

в

б

Рис. 14.19

а

t

Зуб колеса (шестерни) рассматривается (рис. 14.19, а) как консольный, жестко закрепленный одним концом, стержень шириной b и высотой в опасном сечении у основания зуба S_F. Расчет проводят для момента приложения нагрузки в вершине зуба, что соответствует началу зацепления для зубьев ведомых колес и окончанию зацепления для зубьев ведущих колес. Сила нормального давления F_n в месте зацепления равномерно распределена по ширине зуба. Для удобства расчета силу F_n перенесем по линии ее действия до оси симметрии зуба и заменим составляющими: изгибающей F_t' = F_ncosα' и сжимающей F_r' =
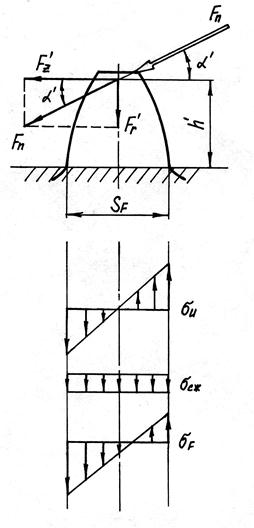
= F_nsinα'; где α' – угол между линией зацепления и нормалью к оси симметрии зуба, в рассматриваемый момент он больше угла зацепления α (α' > α). Зуб испытывает сложное напряженное состояние: сжатие от силы F_r' и изгиб от силы F_t'. Наибольшие напряжения возникают у основания зуба, изгибающий момент М_и для этого сечения максимален. На рис. 14.19 представлены для опасного сечения, т.е. основания зуба, эпюры напряжений при изгибе σ_и (рис. 14.19, б), напряжений сжатия σ_сж (рис. 1.4.19, в) и эпюра результирующих нормальных напряжений σ_F рис. 14.19, г). Установлено, что разрушение всегда начинается на растянутой части зуба, испытывающей растяжение при изгибе. Наибольшее напряжение в опасном сечении с учетом концентрации напряжений и дополнительных динамических нагрузок между зубьями будет

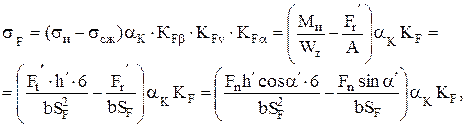(14.22)

а

где М_и = F_t'h' – изгибающий момент у основания зуба от силы F_n; W_z =
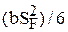= – момент сопротивления сечения у основания зуба относительно нейтральной оси; A = b∙S_F площадь опасного поперечного сечения зуба; α_K – теоретический коэффициент концентрации напряжений (см. п. 5.15.1);
K_F = K_Fβ∙K_Fv∙K_Fα – коэффициент, учитывающий распределение нагрузки (см. рис. 14.18, а, б) по ширине венца (K_Fβ), внутреннюю динамику (табл. 14.6) передач (K_Fv) и распределение нагрузки (табл. 14.7) между зубьями (K_Fα).

в

Используем выражения (14.20, 14.21) для определения F_n через задаваемые при расчетах величины, а именно, передаваемый момент Т и угол зацепления α. После деления и умножения полученного выражения на модуль m, так как размеры зуба всегда выражаются через модуль, зависимость (14.22) примет вид

. (14.23)

Выражение, стоящее в квадратных скобках, обозначим Y_F и назовем коэффициентом прочности, учитывающим форму зуба и концентрацию напряжений. Значения его для зубчатых колес прямозубых цилиндрических передач с нормальной высотой зуба и числом зубьев z и косозубых цилиндрических, конических с эквивалентным числом зубьев z_v приведены в табл. 14.8.

Таблица 14.8

Значения коэффициента Y_F

z (zv)							и более
YF	4,26	4,09	3,90	3,80	3,70	3,62	3,60

Для колес с внутренними зубьями можно принимать Y_F = 3,5 … 4, большие значения соответствуют меньшим z.

Условие прочности зуба на изгиб примет вид

σ_F = (2T₁K_FY_F)/(d₁bm) ≤ σ_Radm, (14.24)

где σ_Radm – допускаемое напряжение зубьев при расчете их на сопротивление усталости при изгибе с коэффициентом асимметрии R цикла нагружения: для реверсивных зубчатых передач σ_Radm = σ_–1/n, для нереверсивных – σ_Radm = = σ₀/n, где σ_–1, σ₀ – предел выносливости материала соответственно при симметричном или отнулевом цикле нагружения; n = 1,3 … 2 – коэффициент запаса прочности.

При одинаковых материалах пары колес расчет на прочность ведут для шестерни (колеса с меньшим числом z₁ зубьев), а при разных материалах – для того из колес, в котором отношение Y_F/σ_Radm больше.

После замен d₁ = mz₁ и b = ψm = (2 … 6)m уравнение (14.24) примет вид

σ_F = (2T₁K_FY_F)/(m³z₁ψ) ≤ σ_Radm, (14.25)

откуда определим величину модуля зацепления

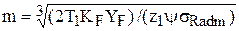. (14.26)

Зависимость (14.25) используют при проверочном расчете, когда задаются предварительно размерами передачи, а зависимость (14.26) – при проектировочном расчете. Полученное из выражения (14.26) значение модуля m округляют до ближайшего большего стандартного значения и определяют остальные параметры передачи, приведенные в подразд. 14.2.

Расчет на усталостную прочность при изгибе проводят только для самой нагруженной тихоходной ступени. Модуль колес остальных ступеней принимают равным модулю тихоходной ступени.

Выбор материала определяется характером нагрузок в передаче, окружной скоростью, сроком службы и условиями эксплуатации.

14.12.3. Проверочный и проектировочный расчеты прямозубой
цилиндрической передачи на контактную усталость

В месте зацепления зубьев (рис. 14.16) периодически под действием силы F_n возникают контактные напряжение σ_Н. Установлено, что усталостное контактное повреждение происходит на поверхностях ножек зубьев вблизи полюсной линии. Контакт зубьев рассматривается как контакт цилиндров с радиусами кривизны ρ эвольвент в полюсе Р зацепления. Максимальные контактные напряжения определяем по формуле Герца (5.89):

, (14.27)

где q – удельная нагрузка; Е_п = 2Е₁Е₂/(Е₁ + Е₂) – приведенный модуль упругости материалов зубьев шестерни (Е₁) и колеса (Е₂) в МПа, при Е₁ = Е₂ = Е, Е_п = Е; ρ_п = ρ₁∙ρ₂/(ρ₁ ± ρ₂) – приведенный радиус кривизны рабочих поверхностей зубьев, знак «–» берут для передачи с внутренним зацеплением; µ – коэффициент Пуассона материала зубьев.

Диаметры делительных d (начальных d_w) окружностей шестерни (d₁ = d_1w) и колеса (d₂ = d_2w) соответственно равны

d₂ = d₁u, (14.28)

где u – передаточное число передачи

Из свойств эвольвенты (подразд. 14.2) известно, что центры ее кривизны лежат на основной окружности, а основные окружности шестерни и колеса касаются линии зацепления. Поэтому (рис. 14.16) радиусы кривизны эвольвент рабочих поверхностей зубьев определим из треугольников О₁ВР и О₂АР: ρ₁ = (d₁∙sinα)/2; ρ₂ = (d₂∙sinα)/2; а приведенный радиус кривизны этих поверхностей с учетом выражения (14.28) равен

ρ_п = (d₁u∙sinα)/(2(u ± 1)). (14.29)

Расчетная удельная нагрузка, приходящаяся на единицу длины контактной линии (ℓ= ε_αb) зубьев шестерни и колеса равна

q = F_nK_H/(ε_αb)= (2T₁K_H)/(d₁ε_αbcosα), (14.30)

где Т₁ – момент на шестерне, Н∙мм; ε_α – коэффициент торцового перекрытия; K_H = K_Hβ∙K_Hv∙K_Hα – коэффициент, учитывающий распределение нагрузки (рис. 14.18, в, г) по ширине венца (K_Hβ), внутреннюю динамику (см. табл. 14.5) передачи (K_Hv) и распределение нагрузки (см. табл. 14.7) между зубьями (K_Hα); α – угол зацепления.

Исходная формула (14.27) с учетом зависимостей (14.28 – 14.30) примет вид

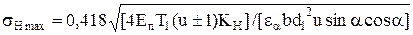. (14.31)

Заменим: ; ; 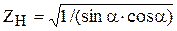b = ψ_bdd₁, где ψ_bd – коэффициент ширины венца b колеса по диаметру делительной окружности.

Коэффициент z_E, учитывающий механические свойства материалов колес, имеет размерность МПа^1/2 для стальных колес с E_п = Е₁ = Е₂ = = 2∙10⁵МПа – z_E = 192; при E_п = 2,15∙10⁵МПа – 195; для зубчатых пар с материалами сталь-бронза z_E = 160; для материалов текстолит-сталь z_E = 49.

Влияние торцового перекрытия учитывают коэффициентом z_ε. Считая, что в зацеплении находится одна пара зубьев, принимают z_ε = 1.

Условие прочности зуба по контактным напряжениям с учетом принятых замен будет

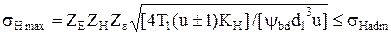. (14.32)

Допускаемые контактные напряжения σ_Hadm принимают равными: для стальных колес – 2,6 НВ; для бронз – (0,75 … 0,9) σ_ut; для текстолитовых колес – (45 … 57) МПа; σ_ut – предел прочности материала при растяжении.

Формула (14.32) используется для проверочного расчета при заданных размерах передачи.

При одновременных проверочных расчетах на усталостную прочность при изгибе (14.25) и по контактным напряжениям (14.32), определяющими считают контактные напряжения σ_H. Это связано с тем, что при заданных размерах колес напряжение σ_F при изгибе можно уменьшить при сохранении размеров за счет увеличения модуля.

Решая уравнение (14.32) относительно диаметра делительной окружности шестерни, получим, учитывая, что T₁ = T₂/u.

. (14.33)

Далее, задавшись числом зубьев шестерни, определяют модуль зацеплении

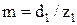. (14.34)

Зависимости (14.33) и (14.34) используют при проектировочном расчете. Рассчитанное значение модуля округляют до ближайшего большего стандартного значения и определяют все размеры передачи (подразд. 14.2).

Дата добавления: 2014-11-29