Прочность прямозубых цилиндрических передач

14.12.1. Расчетная нагрузка, действующая в зацеплении прямозубой
цилиндрической передачи

Расчет зубчатой передачи на прочность ведут, считая, что в зацеплении находится одна пара зубьев шестерни и колеса (см. рис. 14.16). Если пренебречь силами трения в зацеплении из-за их малости, то при расчете учитывают силу нормального давления F_n, лежащую в плоскости зацепления и направленную по общей нормали N-N к соприкасающимся эвольвентным профилям, т.е. вдоль линии зацепления, которая проходит через полюс Р и образует с перпендикуляром к линии центров О₁О₂ угол зацепления α. В стандартном зацеплении он равен 20°. Силу F_n нормального давления и радиальную составляющую F_r можно выразить через окружную силу

F_t = 2T/d, (14.20)

где T – вращающий момент в зацеплении; d – диаметр делительной окружности колеса. Тогда

F_n = F_t/cosα и F_r = F_t∙tgα, (14.21)

где α – угол зацепления.

Направление силы F_t на ведомом колесе совпадает с направлением вращения, на ведущем – противоположно ему. При расчетах номинальную величину F_t умножают на коэффициент К, учитывающий влияние отдельных факторов на расчетную нагрузку: в частности, K = K_β∙K_v∙K_α, где K_β – коэффициент, учитывающий распределение нагрузки по ширине венца; K_v – коэффициент, учитывающий динамичность нагрузки; K_α – коэффициент, учитывающий распределение нагрузки между зубьями. В расчетах используют следующие обозначения: Z – специфические коэффициенты для расчетов на контактную прочность; Y – коэффициенты, используемые только для расчетов на изгиб; индекс Н – для величин, учитываемых при расчете на контактную прочность; индекс F – для величин, используемых при расчете на изгиб.

На рис. 14.17, а показана сила нормального давления F_n, распределенная по длине зуба равномерно. В действительности такое распределение нагрузки маловероятно даже у точно изготовленных передач. Неравномерность распределения нагрузки может быть вызвана упругими деформациями валов, опор и корпусов, зубчатых колес; неточностями изготовления и сборки деталей передач, износом и т.д. Для определения ориентировочных значений K_β в стандарте имеются графики, приведенные на рис. 14.18, где K_Hβ – коэффициент неравномерности при расчете на контактную прочность; K_Fβ – коэффициент неравномерности при расчете на изгиб в зависимости от параметра ψ_bd = b/d, (коэффициента ширины b венца колеса по диаметру d делительной окружности шестерни, рекомендуется ψ_bd = 0,1 … 0,6) и схемы передачи. Каждая из кривых графиков соответствует определенному положению колес относительно опор валов; цифры у кривых соответствуют передачам, указанным на схемах; кривые 1 и 2 –для случаев консольного расположения колес на валах, опирающихся соответственно на шариковые и роликовые подшипники качения. Графики разработаны для режима работы с переменной нагрузкой и окружной скоростью v < 15 м/с. При постоянной нагрузке и твердости Н хотя бы одного из зубчатых колес Н < 350 HB и окружной скорости v < 15 м/с вследствие полной приработки зубьев принимают K_β = 1.

Коэффициент K_v учитывает динамические нагрузки, возникающие в зацеплении из-за погрешностей изготовления, сборки передачи, деформации зубьев, приводящих к непостоянству действительных значений мгновенного передаточного отношения. Величина K_v зависит от степени точности колес, вида передачи, твердости рабочих поверхностей зубьев и окружной скорости колес. Значения K_v для цилиндрических передач, рассчитываемых на контактную прочность, приведены в табл. 14.5 и рассчитываемых на изгиб – в табл. 14.6, при этом в числителе даны значения для прямозубых, а в знаменателе – для косозубых колес.

Таблица 14.5

Значения коэффициента K_Hv

Степень точности зубчатого колеса	Твердость Н поверхности зубьев	Окружная скорость v, м/с
	Н ≤ 350 НВ	1,04/1,01	1,07/1,03	1,14/1,05	1,21/1,06	1,29/1,07	1,36/1,08
Н > 350 НВ	1,03/1,00	1,05/1,01	1,09/1,02	1,14/1,03	1,19/1,03	1,24/1,04
	Н ≤ 350 НВ	1,04/1,01	1,08/1,03	1,16/1,05	1,24/1,06	1,32/1,07	1,40/1,08
Н > 350 НВ	1,03/1,01	1,06/1,01	1,10/1,02	1,16/1,03	1,22/1,04	1,26/1,05
	Н ≤ 350 НВ	1,05/1,01	1,10/1,03	1,20/1,05	1,30/1,07	1,40/1,09	1,50/1,12
Н > 350 НВ	1,04/1,01	1,07/1,01	1,13/1,02	1,20/1,03	1,26/1,04	1,32/1,05

Таблица 14.6

Значения коэффициента K_Fv

Степень точности зубчатого колеса	Твердость Н поверхности зубьев	Окружная скорость v, м/с
	Н ≤ 350 НВ	1,08/1,03	1,16/1,06	1,33/1,11	1,50/1,16	1,62/1,22	1,80/1,27
Н > 350 НВ	1,03/1,01	1,05/1,02	1,09/1,03	1,13/1,05	1,17/1,07	1,22/1,08
	Н ≤ 350 НВ	1,10/1,03	1,20/1,06	1,38/1,11	1,58/1,17	1,78/1,23	1,96/1,29
Н > 350 НВ	1,04/1,01	1,06/1,02	1,12/1,03	1,16/1,05	1,21/1,07	1,26/1,08
	Н ≤ 350 НВ	1,13/1,04	1,28/1,07	1,50/1,14	1,72/1,21	1,98/1,28	2,25/1,35
Н > 350 НВ	1,04/1,01	1,07/1,02	1,14/1,04	1,21/1,06	1,27/1,08	1,34/1,09

Теоретическое значение коэффициента перекрытия из-за погрешностей изготовления деталей передач и упругих деформаций зубьев может не совпадать с его действительным значением. Ориентировочные значения коэффициентов K_Hα и K_Fα, учитывающих распределение нагрузки между зубьями приведены в табл. 14.7.

г

в

б

а

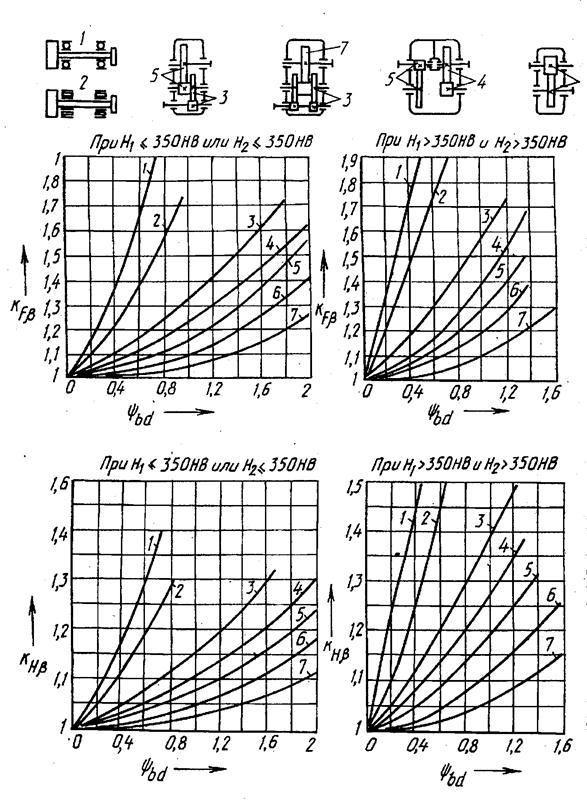
Рис. 14.18

Таблица 14.7

Ориентировочные значения коэффициентов K_Hα и K_Fα

Степень точности колес	Окружная скорость v, м/с
v ≤ 5	5 < v ≤ 10	5 < v ≤ 10
KHα	KFα	KHα	KFα	KHα	KFα
	1,03	1,07	1,05	1,20	1,08	1,25
	1,07	1,22	1,10	1,30	1,15	1,40
	1,13	1,35

При расчетах зубчатых передач на прочность известны: момент нагрузки Т, передаточное число u, числа зубьев колес z и механические свойства материалов колес. Задача состоит в определении модуля зацепления m, через который можно выразить все геометрические размеры передачи.

Дата добавления: 2014-11-29