Расчет на прочность косозубой цилиндрической передачи

Прочность зуба косозубого колеса определяется его формой и размерами в нормальном сечении и длиной зуба. Чтобы унифицировать методику расчетов на прочность прямых и косых зубьев введено понятие эквивалентного колеса. При расчетах на прочность косозубые колеса условно заменяют эквивалентными по прочности цилиндрическими прямозубыми. Эквивалентным прямозубым колесом называют такое колесо, форма и размеры зубьев которого приближенно совпадают с формой и размерами зуба косозубого колеса в нормальном сечении. При этом модуль m_v эквивалентного колеса и нормальный модуль m_n косозубого колеса равны (m_n = m_v), как и длины зубьев этих колес (b= b_v), а радиус делительной окружности эквивалентного колеса равен наибольшему радиусу кривизны эллипса, полученного в сечении делительного цилиндра косозубого колеса (рис. 14.21) плоскостью n – n. Полуоси полученного в сечении эллипса равны c = d/2 и е = d/(2cosβ), где d – диаметр делительной окружности косозубого колеса, β – угол наклона зуба.

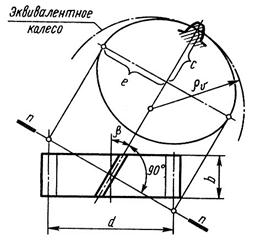Из аналитической геометрии известно, что наибольший радиус кривизны эллипса равен r_v = e²/c = d/(2cos²β). Тогда диаметр делительного цилиндра эквивалентного колеса

d_v = 2r_v = d/cos²β, (14.38)

а число зубьев эквивалентного колеса

z_v = d_v/m_n = d/m_ncos²β = z/cos³β, (14.39)

где d, z – соответственно диаметр делительного цилиндра и число зубьев косозубого колеса. Приведенный радиус кривизны

Рис. 14.21

ρ_п = (d₁u∙sinα)/(2(u ± 1)cos²β); суммарная длина контактных линий ℓ = ε_αb/cosβ.

Рис. 14.21

Вывод зависимостей для проведения прочностных расчетов цилиндрических прямо- и косозубых колес аналогичен. Наклонное расположение зубьев придает косозубым колесам и передачам ряд положительных свойств, в том числе повышенную прочность и плавность, что учитывают при расчетах. В связи с этим при определении изгибных напряжений используем уравнение (14.24), но введем в него коэффициент, учитывающий наклон зуба Y_β = [1 – ε_β(β/120)] ≥ 0,7, где коэффициент осевого перекрытия ε_β = b/p_х , b – ширина венца (рис. 14.21); p_x = p_t/sinβ – осевой шаг, p_t – окружной шаг в торцовом сечении. Тогда уравнение для проверочных расчетов косозубых колес на сопротивление усталости при изгибе примет вид

σ_F = (2T₁K_FY_FY_β)/(m_n³z₁ψ) ≤ σ_Radm, (14.40)

где коэффициент формы зуба Y_F, выбирается из табл. 14.8 по эквивалентному числу зубьев z_v; m_n– нормальный модуль косозубого колеса.

При расчете косозубых колес по контактным напряжениям с использованием уравнений (14.32, 14.33) наклон зуба учитывается коэффициентом форм сопряженных поверхностей Z_H, который для косозубых передач равен 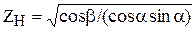. Коэффициент, учитывающий суммарную длину контактных линий определяют как .

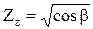Дата добавления: 2014-11-29