Кинематика планетарных редукторов

Передаточное отношение зубчатой передачи, состоящей из двух колес с числом зубьев z₁ и z₂ , равно

i_1,2 = ±z₂/z₁, (15.1)

где знак минус используют при внешнем зацеплении, знак плюс – при внутреннем.

Общее передаточное отношение многозвенного зубчатого механизма с неподвижными геометрическими осями всех колес равно произведению передаточных отношений отдельных механизмов (ступеней), последовательно включенных в его состав:

i_1n = i₁₂ ×i₂₃ ×i₃₄… i_(n–1)n. (15.2)

Чтобы воспользоваться формулами и зависимостями (15.1), (15.2) для зубчатых передач с подвижными геометрическими осями колес при аналитическом исследовании планетарных передач, применяют способ обращенного движения или останова водила. Для этого, не меняя относительного движения звеньев, звеньям условно сообщают дополнительное вращение вокруг центральной оси с угловой скоростью, равной угловой скорости водила, но противоположно направленной. В этом случае водило станет неподвижным и планетарную передачу можно рассматривать как передачу с неподвижными осями колес. Отметим, что угловые скорости полученного обращенного механизма будут отличаться от действительных скоростей планетарного механизма на величину скорости добавочного вращения, т.е. скорости водила (–w_н).

Рассмотрим планетарный механизм (см. рис. 15.2, а). Определим передаточное отношение i_1Н = w₁/w_Н, если числа зубьев колес соответственно равны z₁, z₂, z_2¢ и z₃. Мысленно сообщим всем звеньям дополнительное вращение с угловой скоростью (–w_Н). Механизм обращается в обычный зубчатый (рис. 15.2,в), водило становится неподвижной осью сателлита, центральное колесо z₁ вращается с угловой скоростью w₁^н = w₁–w_Н, а второе центральное колесо z₃, которое было неподвижным, получило скорость w₃^н = –w_Н. Верхний индекс при обозначении угловых скоростей показывает, какое звено неподвижно. Передаточное отношение полученного механизма (см. рис. 15.2, в)

i₁₃^н = w₁^н/w₃^н = (w₁ – w_Н)/(–w_Н) = 1 – i_1Н³, (15.3)

откуда i_1Н³ = 1 – i₁₃^н.

В общем случае передаточное отношение между центральным колесом n и водилом Н при неподвижном центральном колесе k равно

i_nн^k = 1 – i_nk^н, (15.4)

где i_nk^н –передаточное отношение между звеньями n и k обращенного механизма, т.е. механизма с условно неподвижным водилом H.

Согласно зависимостям (15.2) и (15.1), для обращенного механизма

i₁₃^н = i₁₂^н i_{2¢ 3}^н = 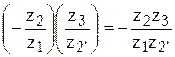. (15.5)

Тогда для рассматриваемого механизма (схема рис. 15.3, б)

i_1Н³ = 1 + 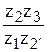. (15.6)

Для планетарных редукторов соответственно:

для схемы (см. рис. 15.3, а)

i_1Н³ = 1 + z₃/z₁, (15.7)

и для схем (см. рис. 15.3, в, г)

i_1Н³ = 1 – 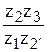. (15.8)

Например, для механизма (см. рис. 15.3, в) при z₁ = z_2¢ = 100; z₂ = 99 и z₃ = = 101 получим i_1Н³ = 1/10000. Но i_Н1³ = 1/ i_1Н³, поэтому передаточное отношение от водила к звену 1 при выбранных числах зубьев i_Н1 = 10000.

Дата добавления: 2014-11-29