Переходные режимы электроприводов

Одной из задач динамики ЭП является задача анализа переходных режимов приводов с АД, которая без учёта электромагнитных пере-ходных процессов решается на основе следующих уравнений (8.5.1 – 8.5.4):

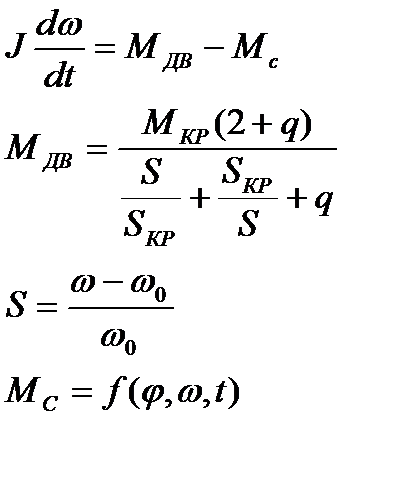
(8.5.1)

(8.5.2)

(8.5.3)

(8.5.4)

где – соответственно синхронная угловая скорость и угловая скорость ротора (вала) двигателя; J – приведённый к валу двигателя сум-марный момент инерции вращающихся и поступательно движущихся частей привода; 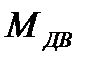– момент двигателя; 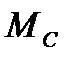– момент сопротивления, создаваемый рабочей машиной, в общем случае может зависеть от угла поворота вала двигателя и его угловой скорости как (12); – скольжение двигателя и его критическое значение соответственно; – критический момент двигателя; Q – константа, зависящая от критическо-го скольжения, кратности критического и пускового момента двигателя.

Аналитически (посредством интегрирования дифференциального уравнения (8.5.4)) система уравнений (8.5.1 – 8.5.4), решается только для

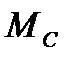= сonst или 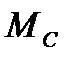= 0. Во всех остальных случаях для её решения ис-пользуют приближённые графоаналитические методы.

Рассматриваемая задача может быть сравнительно просто решена на основе метода структурного моделирования. Покажем это на примере решения задачи, содержание которой следующее.

Для ЭП вентилятора с двигателем типа 4А80В2УЗ имеющего характеритики:

J_ДВ = 0,002кг∙м², S_КР = 0,38, ω= 300,5 рад/с, ω₀ = 314 рад/с, М_КР = 19,03Нм, q= 2,22,

необходимо определить время пуска. Момент сопротивления вентиля-тора

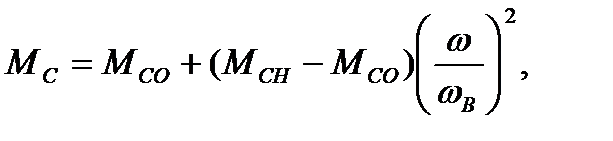
где – начальный момент сопротивления вентилятора;

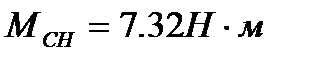– момент сопротивления вентилятора при номинальной угловой скорости 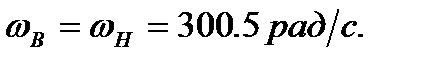Момент инерции вентилятора J=0,06 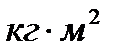, а суммарный момент инерции

Структурная схема соответствующая системе уравнений (8.5.1 – 8.5.4) после записи как

,

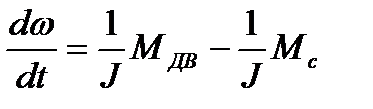будет иметь вид показанный на рис.8.5.1.

График переходного процесса при пуске вентилятора, полученный в результате моделирования на основе структурной схемы рис. 8.5.2, соответствующей структурной модели рис. 8.5.3 приведён на рис. 8.5.4. Анализ результатов показывает, что длительность пуска рассматри-ваемой электромеханической системы (АД – вентилятор) составляет t_П = 0.32 (данное значение t_П взято из числовых результатов расчёта).

+

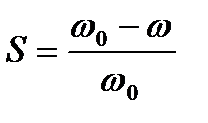
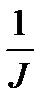
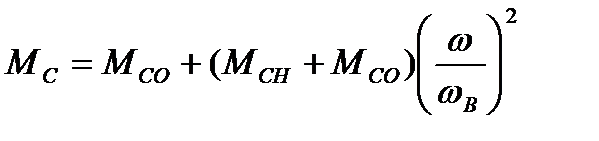
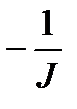
ω

ω

ω

Рис. 8.5.1. Структурная схема модели ЭП с АД

Точность расчёта на основе структурной модели на 20% выше, чем точность результата, полученного графоаналитическим методом ().

Метод структурного моделирования позволяет получать не только графики переходных процессов, но и при необходимости, используя блок фиксации данных «Фазовая плоскость», строить фазовые портреты по любым двум переменным величинам. Для рассматриваемой задачи в результате моделирования можно получить механические характеристи-ки, соответствующие уравнениям (8.5.2 – 8.5.4) рис. 8.5.3.

Построение модели для электропривода вентилятора с двигателем типа 4А80В2У3. Воспользуемся ПП “Mathlab” приложением Simulink.

Рис. 8.5.2. Структурная схема модели ЭП вентилятора

в приложении Simulink

1.Блоки вычисления Fcn, Fcn1, Fcn4 по формулам (8.5.2 – 8.5.4) строим, используя User-DefinedFunctions/Fcn.

2.Блоки вычисления Fcn2, строим, используя User-Defined Functions / Fcn.

3. Блоки вычисления, приведённые в пункте 1, соединяем с помо-щью сумматора, взятого из Math Operations/Sum.

4. Сумматор и интегратор, взятый из Countinuous/Integrator, сое-диняем между собой, используя блок вычисления, приведённый в п. 2.

5. Строим зависимость W = f(М_ДВ), используя блок Sinks/XYGraph.

6. Строим зависимость W = f(t), используя блок Sinks/scope.

Вычисления:

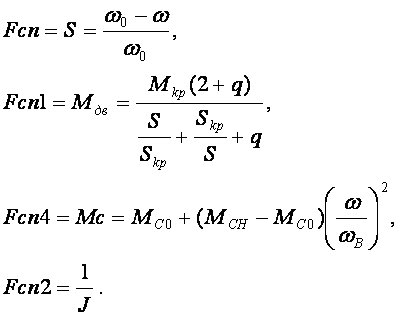
Рис. 8.5.3. Механическая характеристика электродвигателя

Рис. 8.5.4. График переходного процесса пуска вентилятора

Дата добавления: 2014-11-29