Основний принцип комбінаторики

Комбінаторика

Вступ

ЗАВДАННЯ ПО ВИКОНАННЮ РОЗРАХУНКОВО-ГРАФІЧНОЇ

РОБОТИ № 6 " ТЕОРІЯ ЙМОВІРНОСТЕЙ”.

Комбінаторика. Елементи теорії ймовірностей та математичної статистики

У методичних вказівках з курсу «Теорія ймовірностей», частина 1-а відповідно до програми для курсантів усіх спеціальностей ОНМА містяться необхідні теоретичні відомості і формули для розв'язування типових задач, далі наводяться розв'язки типових задач, а також варіанти контрольних завдань за темами «Комбінаторика», «Елементи теорії ймовірностей», “Математична статистика”.

При розв'язуванні задач з теорії ймовірностей згідно з класичним означенням ймовірності випадкової події необхідно підраховувати кількість яких-небудь об'єктів - елементів деяких кінцевих множин або число всіляких способів, за допомогою яких можна здійснити вибір того або іншого результату. Такі задачі вивчає комбінаторика, предметом якої є теорія кінцевих множин.

Нехай з пункту А до пункту В можна проїхати трьома різними видами транспорту, а з В до С - двома:

Необхідно знати, яким числом способів можна проїхати з А до С через В?

Розв'язання.

Очевидно, що число різних шляхів з А до С дорівнює 3*2=6, оскільки для кожного з трьох можливих способів подорожі з А до В маємо два можливих способи подорожі з В до С.

Міркування, що приводяться при розв'язуванні цієї задачі, ілюструють основний принцип комбінаторики. Сформулюємо його.

Основний принцип комбінаторики:

Якщо треба здійснити k-крокову операцію, перший крок якої можна виконати числом 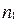способів, другий крок - 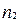числом способів,..., k-ий крок - числом способів, то всю операцію можна здійснити: 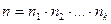числом способів.

Дата добавления: 2014-11-29