Формула повної ймовірності. Формула Байеса

Нехай дана повна група подій, тобто система єдино можливих і несумісних подій ймовірності яких відомі. Нехай, крім того, відомо, що подія Е може настати тільки спільно з однією з подій 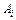, тобто

,

Причому відомі імовірності 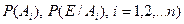. Потрібно знайти імовірність появи події , тобто .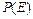

За теоремою додавання імовірностей неспільних подій з попередньої рівності отримуємо

(10)

Ця формула називається формулою повної ймовірності.

Нехай тепер необхідно знайти ймовірності подій в припущенні, що проведено експеримент, в результаті якого появилась подія . Так як наперед невідомо, яка з подій 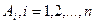наступить, їх називають гіпотезами. Ймовірності таких гіпотез, як умовні ймовірності, шукаємо за формулою 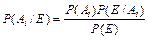. Замінимо тут 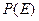за формулою (10), отримаємо .

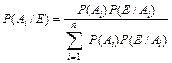Ця формула називається формулою Байеса, або формулою гіпотез, оскільки визначаєймовірність гіпотези, яка полягає в тому, що подія відбулася саме сумісно з подією .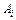

Приклад. Однакові деталі виготовляються на 3-х верстатах. Перший верстат виробляє 50% всіх деталей, другий - 30% і третій - 20%. При цьому ймовірність браку на першому верстаті дорівнює 0,025, на другому 0,02, на третьому - 0,015. Знайти ймовірність того, що навмання взята з комори деталь виявиться доброякісною.

Розв'язання.

Визначимо через, , 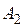і події, які полягають в тому, що деталь виготовлена відповідно на 1-ому, 2-ому і 3-ому верстатах. Тоді

Подія, яка полягає в тому, що деталь виявиться доброякісною, визначимо буквою 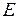. Тоді

По формулі повної ймовірності знаходимо

4.2.6. Повторення незалежних випробувань. Формула Бернуллі. Теорема Пуассона. Локальна і інтегральна теореми Лапласа

Ряд випробувань будемо називати незалежними по відношенню до події , якщо ймовірність появи події в кожному випробуванні не залежить від результатів інших випробувань.

Приклади незалежних випробувань: 1) кидання монети або грального кубика; 2) стрільба по цілі без коректування в одних і тих же умовах; 3) багаторазове витягання з урни кулі за умовою, що вийнята куля після реєстрації її кольору повертається зворотно в урну і кулі після цього перемішуються.

Приклад.

Нехай проводиться n незалежних випробувань, внаслідок кожного з яких подія може статися з ймовірністю . За цими припущеннями розглянемо наступні ймовірності.

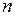1. Знайти ймовірність того, що подія наступить у всіх випробуваннях.

Розв'язання. Оскільки випробування незалежні, то за теоремою про добуток ймовірностей отримаємо

.

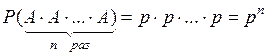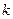2. Знайти ймовірність того, що подія станеться в перших випробуваннях і не станеться у 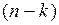випробуваннях, що залишилися.

Розв'язання.

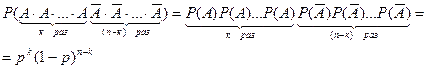
3. Знайти ймовірність здійснення події 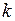разів в будь-якому порядку у 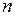випробуваннях.

Розв'язання. На відміну від попередньої задачі тут 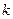номерів випробувань, в яких реалізовується подія можуть бути довільними. Число комбінацій з 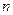елементів по 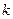дорівнює числу сполучень . Тому шукана ймовірність дорівнює

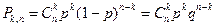, (12)

де .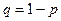

Формула (12) називається формулою Бернуллі.

Для так званих рідкісних подій (зі значеннями 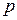близькими до нуля) користуються асимптотичною формулою Пуассона:

, (13)

де 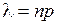і наближення тим краще, чим більше 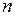і менше .

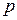Для двозначного числа 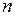(тобто, коли n є великим числом) повторних випробувань обчислення ймовірності за формулою Бернуллі викликає обчислювальні труднощі так, як при цьому громіздко обчислюється . Тому в таких випадках застосовується наступна наближена формула

, (14)

що виражає зміст локальної теореми Лапласа, де .

Приклад. Ймовірність влучення у ціль при одному пострілі рівна 0,7. Яка ймовірність того, що з 20 пострілів 15 виявляться влучними?

За формулою (12) знаходимо .

За формулою (14)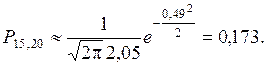

Інтегральна теорема Лапласа. Нехай знову проводиться n незалежних випробувань, внаслідок кожного з яких подія може статися з ймовірністю (0<р<1). При цих припущеннях знайдемо ймовірність того, що подія А з'явиться в n випробуваннях не менш 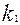і не більш 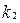разів приблизно дорівнює визначеному інтегралу

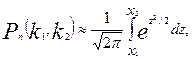(15)

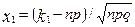де і .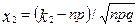

Функція - отримала назву функції Лапласа

Ця функція є непарною. Для функції складені таблиці її значень.

4.2.7.Випадкові величини і їх закони розподілу

Випадковою величиною називається змінна, яка може приймати внаслідок випробування те або інше значення, невідоме заздалегідь (до випробування) - яке саме.

Конкретні значення, які може приймати випадкова величина, називаються можливими її значеннями. Значення випадкової величини залежить від результату випробування, тобто від елементарної події. Тому випадкову величину можна визначити як функцію, задану в просторі елементарних подій.

Випадкову величину, всі можливі значення якої неперервно заповнюють деякий проміжок, називають неперервною випадковою величиною. Якщо ж кожне можливе значення випадкової величини може бути пронумероване тобто записане у вигляді послідовності , то таку випадкову величину будемо називати дискретною.

Законом розподілу випадкової величини називається всяке співвідношення, що встановлює зв'язок між можливими значеннями випадкової величини та їх відповідними ймовірностями. Закон розподілу дискретної випадкової величини може бути заданий таблицею, названою рядом розподілу.

Закон розподілу неперервної випадкової величини неможливо задати таблицею, оскільки не можна скласти перелік усіх її можливих значень. Для задання закону розподілу ймовірностей неперервної випадкової величини Х неможливо скористатися ймовірністю події , тому розглядаємо ймовірність події , де - деяка поточна змінна. Ймовірність цієї події, тобто 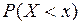, очевидно є деяка функція від . Ця функція називається функцією розподілу випадкової величини 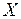і позначається :

.

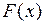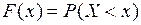Функцію розподілу іноді називають інтегральною функцією розподілу або інтегральним законом розподілу.

Очевидно, функцію розподілу можна знайти і для дискретної випадкової величини 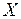, тобто функція розподілу - універсальний спосіб завдання закону розподілу випадкової величини.

Властивості функції розподілу:

1) Значення функції розподілу належать сегменту [0; 1], тобто .

2) Ймовірність того, що випадкова величина набуде значення на напівінтервалі 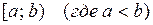, дорівнює різниці значень функції розподілу на кінцях цього інтервалу, тобто

.

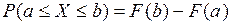3) Функція розподілу є неспадною: якщ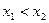о , то .

Дата добавления: 2014-11-29