Системи випадкових величин

Часто результат випробування описується не однією випадковою величиною X, а декількома випадковими величинами: 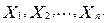У цьому випадку прийнято говорити, що зазначені випадкові величини утворять систему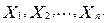

Систему двох випадкових величин (X,Y)можна зобразити випадковою точкою на площині.

Математичні сподівання дискретних випадкових величин X і Y, що входять у систему, визначаються за формулами:

де 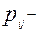ймовірності події, що заключаються в одночасному виконанні рівностей

аматематичні сподівання неперервних випадкових величин за формулами:

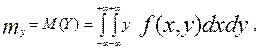
Точка називається центром розсікання системи випадкових величин (X,Y).

Дисперсії дискретних випадкових величин X і Y визначаються за формулами:

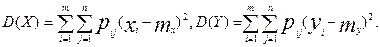
Дисперсії ж неперервних випадкових величин X і Y, що входять у систему, знаходяться за формулами:

Середні квадратичні відхилення випадкових величин X і У визначаються за формулами:

Для обчислення дисперсій можуть бути застосовані формули

Важливу роль у теорії систем випадкових величин грає так називаний кореляційний момент (коваріація)

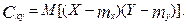
Для дискретних випадкових величин кореляційний момент знаходиться зо формулою:

для неперервних - за формулою:

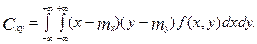
Кореляційний момент можна також знайти за формулою

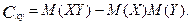
Тут для дискретних випадкових величин X і Y і для неперервних величин.

Випадкові величини X і Y називаються незалежними, якщо ймовірність однієї з них приймає значення, що лежить у будь-якому проміжку області її значень та не залежить від того, яке значення прийняла інша величина. У цьому випадку

Для характеристики зв'язку між величинами X і Y розглядається так названий коефіцієнт кореляції .

4.3. Зразок виконання розрахунково-графічної роботи № 6

Дата добавления: 2014-11-29