Введение в теорию статистических решений

НЕПОРОГОВЫЕ МЕРЫ ЧУВСТВИТЕЛЬНОСТИ

Современные методы измерения чувствительности сенсорных систем, появившиеся из приложения к задачам психофизики теории обнаружения сигнала и теории статистических решений, не используют понятия «порог ощущения» в том виде, как его понимали в классической психофизике. Это привело к разработке принципиально новых подходов к измерению чувствительности, в основе которых лежат следующие основные представления:

- процесс формирования образа является стохастическим процессом (т.е. носит вероятностный характер), причем причиной этого является в основном собственные особенности сенсорной системы;

- в функционировании сенсорной системы можно выделить два основных компонента, которые образуют единое целое – во-первых, собственно сенсорный процесс в его привычном традиционном смысле и, во-вторых, внесенсорную часть, включающую в себя процессы принятия решения и связанную с целями, мотивацией и иными, так называемыми несенсорными факторами.

Предложенные в русле этого подхода меры чувствительности сенсорной системы кардинально отличаются от традиционных пороговых и носят непороговый характер. Для их получения разработаны специальные методы и процедуры, рассмотрение которых требует предварительного ознакомления с основами теории статистических решений.

(теория принятия решений в неопределенных ситуациях)

Большая часть жизненных ситуаций и обстоятельств, в которых приходится действовать человеку, являются неоднозначными - т.е. когда возможно различное толкование обстоятельств и, соответственно, выполнение тех или иных действий. Причины такой «неоднозначности» могут корениться как вовне – в неопределенности объективных жизненных обстоятельств и условий деятельности (либо в неполноте информации о реальных событиях, которую получает человек), так и внутри самого человека – в недостатке возможностей, знаний или желания разобраться в ситуации.

Действия человека в этих условиях будут существенно отличаться от действий в детерминистических обстоятельствах (т.е. допускающих однозначное толкование), в которых существует или может быть найден четкий алгоритм действий. Поведение и деятельность в вероятностной (стохастической, неопределенной) внешней среде требует от субъекта включения в работу новых элементов и процессов, и в первую очередь усложнение коснется процессов принятия решений. В самом простом виде линейная схема процессов построения поведенческого акта в

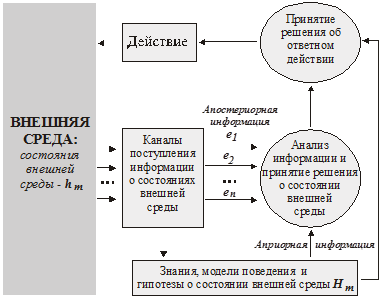интересующей нас части будет выглядеть следующим образом (см. рис.5).

Рис.5. Схема построения поведенческого акта при деятельности в неопределенных условиях (пояснения см. в тексте)

В приведенной на рис.5 схеме использованы следующие обозначения:

h₁, h₂,…, h_m – все возможные состояния реальной внешней среды, одно из которых является актуальным (т.е. существующим) в текущий момент времени;

H₁, H₂,…, H_m – гипотезы о состояниях внешней среды.

e₁, e₂,…, e_n – апостериорная информация о текущем состоянии внешней среды – то есть те сведения, которые субъект получает путем непосредственного наблюдения за средой, от других людей, из средств массовой информации и т.д.;

Приведем четыре примера таких ситуаций, с которыми может столкнуться субъект, но, естественно, в их упрощенном варианте:

Ситуация	«Покупатель»	«Террорист»	«Охотник»	«Измерение»
Описание ситуации	Покупатель идет по рынку и вдруг видит очень нужный товар, который он долго искал …	С борта самолета получают сообщение о террористе, под угрозой взрыва самолета требующего деньги…	Охотник отправился охотиться на зайцев. Проходя через поляну, услышал в кустах шорох…	При измерении чувствительности в интервале наблюдения может быть предъявлен (или нет) стимул.
Проблема	Купить или не купить?	Платить или не платить?	Стрелять или не стрелять?	Был или нет предъявлен стимул.
Цель	Приобрести нужный товар за приемлемую цену	Сохранить жизни пассажиров, не по-нести убытков.	Добыть больше зайцев при минимуме расхода патронов.	Максимально правильно обнаруживать стимул.
Состояние среды	h1	Товар качественный.	У террориста есть бомба.	В кустах есть заяц.	Стимул был (S).
h2	Товар – подделка.	Бомбы нет.	В кустах нет зайца.	Стимула не было (n).
Гипотезы о состоянии среды	H1	Товар качественный.	Есть бомба.	Есть заяц.	Стимул был. (Ответ «Да»)
H2	Товар некачественный.	Нет бомбы.	Нет зайца.	Стимула не было.(Ответ «Нет»)
Апостериорная информация	e1	Товар выглядит качественно.	Личность террориста установлена – мужчина, одинок, безработный, 34 года.	Слышен шорох.	Сенсорное событие (s).
e2	Цена доступная.	На учете у психиатра не состоит.	Шороха нет.
e3	Другие покупатели прицениваются, но никто не покупает.	При прохождении контроля при посадке ничего не было обнаружено.
e4	Продавец слишком настойчиво рекомендует купить.	Проходил спецподготовку во время службы в армии.

Главная задача, которую решает человек при принятии решения в каждой из этих ситуаций, – выбор правильной гипотезы (представления) о состоянии среды и, соответственно, выполнение в последующем действий, которые приведут к достижению желаемой цели. При этом имеется в виду, что принимающий решение не имеет полной и исчерпывающей информации о состоянии среды. Если такая информация есть, то принятие решения редуцируется до простой детерминированной процедуры. Например, в ситуации «Покупатель» такой информацией может быть обнаружение у товара явного дефекта, в ситуации «Охотник» – охотник увидел зайца своими глазами, - то есть поступившей информации достаточно для достоверного подтверждения истинности одной из выдвинутых гипотез H₂ или H₁.

В случае же, когда ситуация неопределенна (неоднозначна), принятие решения начинает осуществляться по законам, которые описываются теорией статистических решений.

Основная задача, которую решает теория статистических решений, – проверка истинности (правдоподобности) гипотез H_i о состоянии среды на основании поступившей информации e_j о реальном состоянии среды h_i. (Полагаем 0 £ i £ m; 0 £ j £ n).

При этом главным является вопрос о правилах (процедурах), на основании которых можно принять или отклонить гипотезу – т.е. принять решение.

3.1.1. Правило принятия решения

В теории статистических решений существует очень простое и вместе с тем достаточно общее решающее правило. Однако, прежде чем сформулировать его, необходимо определить ряд новых понятий, которые позволят дать вероятностное описание ситуации.

Еще до попадания в ситуацию, в которой будет необходимо принимать решение, у человека имеются определенные знания, представления и предположения о ней. Можно сказать, что у субъекта формируется некоторая предвосхищающая модель ситуации (среды), в которой ему предстоит действовать. Совокупность этих знаний и представлений независимо от их источника, будем называть априорной информацией (т.е. полученной априори, «до опыта»). Если речь идет о конкретных событиях, которые должны произойти в будущем, и относительно которых у субъекта есть некоторая априорная информация, то можно говорить об априорной вероятности этих событий. Априорная вероятность – это сформированная на основе имеющейся априорной информации оценка возможности наступления события в будущей ситуации, в которой предстоит принимать решение. Обозначаются априорные вероятности q.

Как правило, предполагается, что субъект формирует оценку априорных вероятностей q_i=p(h_i) возможных состояний среды h_i, так как в любой ситуации человек стремится спрогнозировать дальнейшее развитие событий. Поскольку множество этих состояний образует полную систему событий, то сумма их априорных вероятностей должна быть равна единице:

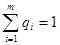. (4)

Априорные вероятности человек оценивает до получения информации о состоянии среды e_j, основываясь на своих знаниях, представлениях, ранее полученной информации и т.д.

Так, в примере «Охотник» априорные вероятности наличия зайца в лесу q₁=p(h₁), и его отсутствия там q₂=p(h₂) могут определяться охотником на основании рассказов местных жителей из соседней деревни или его воспоминаний о прошлой охоте в этом лесу, и т.д. Другими словами, q₁ и q₂ отражают оценку охотником возможности существования состояния среды h₁ (заяц есть) состояния h₂ (зайца нет) еще до того, как он отправился в лес на охоту.

После получения информации e_j самое важное изменение знаний о среде будет состоять в том, что уже существующие априорные вероятности p(h_i) перейдут в апостериорные вероятности p(h_i /e_j).

Апостериорная вероятность p(h_i /e_j) - вероятность того, что действительно может иметь место состояние среды h_i с учетом полученной информации e_j. То есть это представления субъекта о возможном состоянии среды, опирающееся на его предварительные (априорные) знания о ней, но уже скорректированные, измененные с учетом поступившей (апостериорной) информации.

В примере «Охотник» p(h₁/e₁) отражает субъективную вероятность наличия в кустах зайца после того, как охотник услышал оттуда шорох, p(h₂/e₁) -. субъективную вероятность отсутствия зайца при наличии шороха, p(h₂/e₂) – субъективную вероятность отсутствия зайца при отсутствии шороха, p(h₁/e₂) – субъективную вероятность наличия зайца при отсутствии шороха.

Эти величины (апостериорные вероятности) являются основной информацией, на которой базируется принятие решения.

Правило принятия решения в этом случае состоит в том, чтобы сравнить между собой апостериорные вероятности различных гипотез и принять ту из них, для которой апостериорная вероятность наибольшая.

Для самого простого случая, когда возможны только два состояния среды (h₁ и h₂) и, соответственно, высказывается простая двухальтернативная гипотеза (H₁ и H₂), правило принятия решения выглядит следующим образом:

если p(h₁ /e_j) > p(h₂ /e_j), то принимается гипотеза H₁,

если p(h₁ /e_j) < p(h₂ /e_j), то принимается гипотеза H₂.

Таким образом, смысл правила принятия решения состоит в том, что принимается наиболее вероятная гипотеза с учетом полученной информации e_j.

Вербальная формулировка решающего правила может быть следующей:

- если с учетом поступившей апостериорной информации e_j вероятность существования состояния среды h₁ будет больше вероятности существования состояния h₂, то принимается гипотеза H₁;

- если с учетом поступившей апостериорной информации e_j вероятность существования состояния среды h₁ будет меньше вероятности существования состояния h₂, то принимается гипотеза H₂.

На основании теоремы Байеса имеем:

P(h₁ /e_j) = 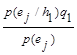, (5)

и решающее правило можно теперь записать так:

Если 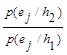< 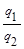, то принимаем H₁; (6 a)

Если 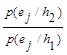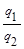, то принимаем H₂. (6 b)

Здесь: p(e_j /h₂) – вероятность того, что появление апостериорной информации e_j вызвано состоянием среды h₂;

p(e_j /h₁) – вероятность того, что появление апостериорной информации e_j вызвано состоянием среды h₁.

Используем следующие обозначения:

λ (e_j) = 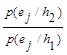; (7)

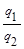λ₀ = . (8)

Вновь введенные величины получили названия:

λ(e_j ) – отношение правдоподобия,

Дата добавления: 2014-11-29