Відношення еквівалентності

Відношення R називається відношенням еквівалентності, якщо воно має наступні властивості:

а) рефлективності: (x, х) Î R при будь-якому х Î Х;

б) симетричності: з (x ₁, х ₂) Î R випливає (x ₂, х ₁) Î R;

в) транзитивності: якщо (x ₁, х ₂) Î R і (x ₂, х ₃) Î R, то (x ₁, х ₃) Î R;

Замість того, щоб писати (x ₁, х ₂) Î R, часто пишуть x ₁ ~ x ₂ або x ₁ º x ₂(mod R) (читається так: x ₁ конгруентно x ₂ за модулем R) чи, простіше, (x ₁ ~ x ₂ або x ₁ º x ₂, якщо немає необхідності ще раз вказувати, що мова йде про одне й те саме відношення R).

Приклади: 1) Беремо множину Z цілих чисел. Будуємо множину X = {(p, q) Î Z ´ Z | q ¹ 0}Відношення еквівалентності задаємо наступним чином: (p, q) º (р', q') якщо рq' - р'q = 0.

2)°Визначимо на множині цілих чисел Z відношення еквівалентності так, що р º q, тоді і тільки тоді, коли p - q ділиться без остачі на деяке наперед задане число m. У теорії чисел таке відношення записується у вигляді р º q (mod т).

3)°Нехай Х - множина прямих на площині. Визначимо відношення еквівалентності для прямих x ₁ і x _2, покладаючи x ₁ º x ₂, коли ці прямі паралельні чи співпадають.

4)° Х – множина всіх векторів 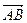на площині. Визначимо на X відношення еквівалентності ~ , якщо ці вектори паралельні, однаково напрямлені й мають однакову довжину.

5)°У тій же множині Х (див.4) встановимо відношення еквівалентності ~ , якщо і лежать на одній прямій, однаково напрямлені й мають однакову довжину.

6) Нехай Х – множина всіх студентів, які присутні на лекції з дискретної математики. Два студенти еквівалентні, якщо вони народилися в тому самому місяці року.

Відношення еквівалентності на множині Х породжує деяке розбиття цієї множини, блоки якого називаються класами еквівалентності. Будь-які два елементи з одного класу зв’язані відношенням еквівалентності, тобто еквівалентні;з різних класів - не еквівалентні.

Побудуємо розбиття множини Х,яке відповідає заданому відношенню еквівалентності на цій множині. Для x Î X позначимо через K (x)підмножину, що складається з елементів, еквівалентних x, тобто K (x) = { y | y Î X; y ~ x }.

Справедлива наступна теорема:

Теорема I. Два класи еквівалентності не перетинаються або співпадають.

Доведення. Припустимо, що перетин множин K (x)і K (х')непорожній, і візьмемо z Î K (x) Ç K (х'). Клас еквівалентності K (x) утворений з елементів, еквівалентних одному зі своїх елементів x. Оскільки x і z еквівалентні, то за властивістю транзитивності отримуємо, що K (x) утворений також з елементів, еквівалентних z. Аналогічно K (х') утворений з елементів, еквівалентних z. Таким чином, K (х) і K (х') співпадають.

З наведеного доведення бачимо, що клас еквівалентності є множиною всіх елементів, еквівалентних довільному елементу з цього класу. Таким чином, клас еквівалентності визначає деяке розбиття множини Х, тобто деяку сім’ю непорожніх підмножин множини X, які попарно не перетинаються,а їхоб’єднання рівне X. Якщо відомі ці підмножини, то відоме й відношення еквівалентності, бо х і х' еквівалентні тоді і тільки тоді, коли вони належать одному класу еквівалентності.

Навпаки, будь-яке розбиття множини X: Х = 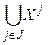, де X_j непорожні і попарно не перетинаються, визначає деяке відношення еквівалентності, а саме x º х', якщо існує такий індекс j Î J, що x Î X_j, х' Î X_j. У цьому випадку підмножини X_j є класами еквівалентності в цьому відношенні.

Зокрема, якщо відображення f: Х ® Y сюр’єктивне, то відношення x ~ y при f (x) = f (y) є відношенням еквівалентності на множині Х і підмножини f ^-1{z}, z Î Y, є класами еквівалентності.

Дата добавления: 2014-11-29