Відношення

Розглянемо декартовий добуток к- го степеня множини Х: Х^к = Х ´ Х ´... ´ Х. Довільну підмножину R множини Х^к (R Í Х^к) будемо називати к -арним відношенням, заданим на множині Х. Вважатимемо, що впорядковані елементи x ₁, x ₂, …, x_n Î Х знаходяться між собою у відношенні R, коли (x ₁, x ₂, …, x_n) Î R. Одномісні відношення, які ще називаються унарними, відповідають підмножинам множини X. Надалі особливу увагу будемо приділяти бінарним відношенням (k = 2), які для стислості будемо називати просто відношеннями, якщо не обумовлено противного. Якщо на Х задано відношення R Í X ², то запис x R х' означає, що x і х' знаходяться у відношенні R, тобто(x, х') Î R.

Областю визначення відношення R називаємо множину d_R = { x | $ y: (x, y) Î R }, а областю значень - множину r_R = { x | $ y: (y, x) Î R }. Для відношень звичайним чином визначені теоретико-множинні операції об’єднання, перетину і т.д. Доповненням відношення R Í X ² вважаємо множину 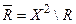. Оберненим відношенням до відношення R називається відношення, задане множиною R ^-1 = {(x, y) | (y, x) Î R }. Образом множини Х відносно R називається множина R (Х) = { y | існує таке х Î Х, що(х, у) Î R } прообразом Х відносно R - множина R ^-1(Х) = { х | існує таке y Î Х, що (х, у) Î R }.

Розглянемо кілька прикладів найпростіших відношень:

1) на множині N відношення £. Ясно, що впорядковані пари (3, 7) і (5, 5) належать цьому відношенню, а пара (4, 1) не належить;

2) на множині Р (Х) всіх підмножин множини Х = {1, 3, 5, 7, 9} відношення Í. Пари підмножин ({1, 3}, {1, 3, 9}) і ({5, 7, 9}, {5, 7, 9}) належать цьому відношенню, а пара підмножин ({1, 5, 7}, {3, 5, 9}) не належить.

Кожному відношенню R на скінченній множині з n елементів X = { x ₁, x ₂, …, x_n } можна поставити у відповідність матрицю А = (а_ij), i, j = 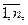де a_ij = 1, якщо x_i R x_j, і a_ij = 0 у протилежному випадку. Матриця А, яка складається з елементів0та1, називається матрицею інцидентності відношення R.

Ця матриця однозначно задає відношення на скінченних множинах. Наприклад, - одинична матриця задає відношення рівності; - якщо в матриці на головній діагоналі знаходяться 0, а інші елементи рівні 1, то вона задає відношення нерівності. Якщо Х = {1, 2, 3, 4} і R – відношення £, то матриця інцидентності матиме вигляд

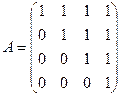
Відношення R на множині X називається:

1) рефлективним, якщо довільний елемент множини знаходиться у відношенні сам з собою, тобто для будь-якого х Î Х виконується х R х. Прикладами рефлективних відношень можуть бути ≤, ≥, = на множині натуральних чисел;

2) антирефлективним, якщо для будь-якого х Î Х пара (х, х) не належить до відношення R. Прикладами антирефлективних відношень можуть бути <, >, ≠ на множині раціональних чисел;

3) симетричним, якщо для довільних x, х ' Î Х з того, що x R x випливає х ' R x;

4) антисиметричним, якщо для довільних x, х ' Î Х з того, що x R х ' і х ' R x, випливає x = х ' (наприклад, £ на N, тому що з x £ х ' і х ' £ x випливає х ' = x);

5) транзитивним, якщо для довільних x, х ', х '' Î Х з того, що x R х ' і х ' R х '', випливає x R х '' (наприклад, відношення Í на множині Р (Х) чи відношення £ на множині N).

Наведемо деякі приклади відношень:

1) рефлективне, симетричне, не транзитивне

R = {(x, х ') | x, х ' Î R, | x - х ' | £ 1};

2) рефлективне, антисиметричне, не транзитивне

R = {(x, х ') | x, х ' Î Z, x £ х ' £ x ²};

3) рефлективне, антисиметричне, транзитивне

R = {(x, х ') | x, х ' Î Q, x £ х '};

4) нерефлективне, антисиметричне, транзитивне

R = {(x, х ') | x, х ' Î R, x = х ' = 0};

5) нерефлективне, симетричне, транзитивне

R = {(x, х ') | x, х ' Î R, x, х ' > 0}.

Будь-якому відношенню R на множині Х можна поставити у відповідність відношення 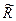, що визначається так: x 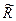х ' для x, х ' Î X, якщо існують такі x ₁, x ₂, …, x_t Î X, що x R x ₁, x ₁ R x ₂,..., x_t R x '. Відношення 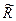називається транзитивним замиканням відношення R. Якщо R транзитивне, то 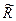= R.

Розглянемо далі відношення, які мають особливе значення.

Дата добавления: 2014-11-29